
【题目】如图,在平面直角坐标系中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数y=![]() 的图象相交于点B(m,1).
的图象相交于点B(m,1).
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
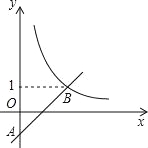
【答案】(1) B(2,1);y=x﹣1;(2) P(0,1)或(0,3).
【解析】
试题分析:(1)由点在函数图象上,得到点的坐标满足函数解析式,利用待定系数法即可求得;
(2)分两种情况,一种是∠BPA=90°,另一种是∠PBA=90°,所以有两种答案.
试题解析:(1)∵B在的图象上,
∴把B(m,1)代入y=![]() ,得m=2,
,得m=2,
∴B点的坐标为(2,1),
∵B(2,1)在直线y=ax﹣a(a为常数)上,
∴1=2a﹣a,
∴a=1,
∴一次函数的解析式为y=x﹣1;
(2)过B点向y轴作垂线交y轴于P点.此时∠BPA=90°,
∵B点的坐标为(2,1),
∴P点的坐标为(0,1),
当PB⊥AB时,在Rt△P1AB中,PB=2,PA=2,
∴AB=![]() ,
,
在等腰直角三角形PAB中,PB=PA=![]() ,
,
∴PA=![]() =4,
=4,
∴OP=4﹣1=3,
∴P点的坐标为(0,3),
∴P点的坐标为(0,1)或(0,3).



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
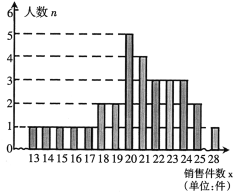
【题目】商场对每个营业员在当月某种商品销售件数统计如下:
解答下列问题
(1)设营业员的月销售件数为x(单位:件),商场规定:当x<15时为不称职;当15≤x<20时为基本称职;当20≤x<25为称职;当x≥25时为优秀.试求出优秀营业员人数所占百分比;
(2)根据(1)中规定,计算所有优秀和称职的营业员中月销售件数的中位数和众数;
(3)为了调动营业员的工作积极性,商场决定制定月销售件数奖励标准,凡达到或超过这个标准的营业员将受到奖励。如果要使得所有优秀和称职的营业员中至少有一半能获奖,你认为这个奖励标准应定为多少件合适?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
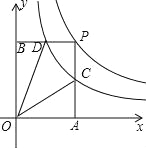
【题目】如图是函数y=![]() 与函数y=
与函数y=![]() 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y=![]() 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y=![]() 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y=![]() 的图象于点D.
的图象于点D.
(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com