【题目】如图，在△ABC中，AD是高，在线段DC上取一点E，使DE=BD，已知AB+BD=DC． 求证：E点在线段AC的垂直平分线上．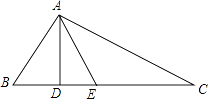
【答案】证明：∵AD是高，∴AD⊥BC， 又∵BD=DE，
∴AD所在的直线是线段BE的垂直平分线，
∴AB=AE，
∴AB+BD=AE+DE，
又∵AB+BD=DC，
∴DC=AE+DE，
∴DE+EC=AE+DE
∴EC=AE，
∴点E在线段AC的垂直平分线上
【解析】根据线段的垂直平分线性质求出BD=DE，推出DE+EC=AE+DE，得出EC=AE，根据线段垂直平分线性质推出即可．
【考点精析】本题主要考查了线段垂直平分线的性质的相关知识点，需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能正确解答此题．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】阅读材料：
小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2
=（1+
）2．善于思考的小明进行了以下探索：
设a+b
=（m+n
）2（其中a、b、m、n均为整数），则有a+b
=m2+2n2+2mn
．
∴a=m2+2n2，b=2mn．这样小明就找到了一种把类似a+b
的式子化为平方式的方法．
请你仿照小明的方法探索并解决下列问题：
（1）当a、b、m、n均为正整数时，若a+b
=
，用含m、n的式子分别表示a、b，得：a=__，b=__；
（2）利用所探索的结论，找一组正整数a、b、m、n填空：__+__
=（___）+__
）2；
（3）若a+4
=
，且a、m、n均为正整数，求a的值？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将长方形ABC沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E． 
（1）试判断△BDE的形状，并说明理由；
（2）若AB=4，AD=8，求AE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有（ ）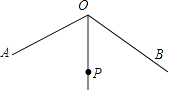 
A.1个
B.2个
C.3个
D.3个以上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com