
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( ) 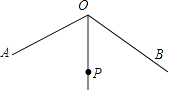
A.1个
B.2个
C.3个
D.3个以上
【答案】D
【解析】解:如图在OA、OB上截取OE=OF=OP,作∠MPN=60°. 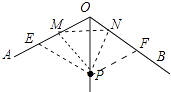
∵OP平分∠AOB,
∴∠EOP=∠POF=60°,
∵OP=OE=OF,
∴△OPE,△OPF是等边三角形,
∴EP=OP,∠EPO=∠OEP=∠PON=∠MPN=60°,
∴∠EPM=∠OPN,
在△PEM和△PON中, ,
,
∴△PEM≌△PON.
∴PM=PN,∵∠MPN=60°,
∴△PNM是等边三角形,
∴只要∠MPN=60°,△PMN就是等边三角形,
故这样的三角形有无数个.
故选D.
如图在OA、OB上截取OE=OF=OP,作∠MPN=60°,只要证明△PEM≌△PON即可推出△PMN是等边三角形,由此即可对称结论.


科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AD∥BC,DB=DC=EC,∠A=2∠ADB,AD=m,AB=n.
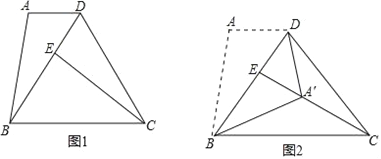
(1)在图1中找出与∠ABD相等的角,并加以证明;
(2)求BE的长;
(3)将△ABD沿BD翻折,得到△A′BD.若点A′恰好落在EC上(如图2),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )
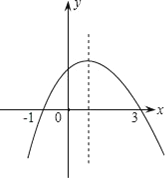
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
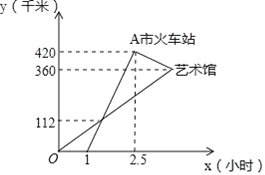
【题目】高铁的开通,给N市市民出行带来了极大的方便,“元旦”期间,甲、乙两人应邀到A市的艺术馆参加演出,甲乘私家车从N市出发1小时后,乙乘坐高铁从N市出发,先到A市火车站,然后再转乘出租车到A市的艺术馆(换车时间忽略不计),两人恰好同时到达A市的艺术馆,他们离开N市的距离y(千米)与乘车时间x(小时)的关系如图所示,请结合图象解答下列问题:
(1)高铁的平均速度是每小时多少千米?
(2)分别求甲、乙(乘坐高铁时)两人离开N市的距离y与乘车时间x的函数关系式;
(3)若甲要提前30分钟到达艺术馆,那么私家车的速度必须达到多少千米/小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com