
【题目】如图1,在四边形ABCD中,AD∥BC,DB=DC=EC,∠A=2∠ADB,AD=m,AB=n.
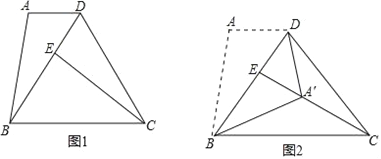
(1)在图1中找出与∠ABD相等的角,并加以证明;
(2)求BE的长;
(3)将△ABD沿BD翻折,得到△A′BD.若点A′恰好落在EC上(如图2),求![]() 的值.
的值.
【答案】(1)见解析 (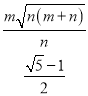 2)
2)![]() (3)
(3)![]()
【解析】(1)由平行线的性质知∠DBC=∠ADB,由DB=DC,得出∠DCB=∠DBC=∠ADB,由DC=EC,得出∠CDE=∠CED=∠DBC+∠BCE=∠ADB+∠BCE,再由三角形内角和定理即可得出结果;
(2)在BC上取一点F,使CF=AB=n,连接EF,由SAS证得△ABD≌△FCE,得出∠EFC=∠DAB=2∠ADB,∠FEC=∠ADB,EF=AD=m,推出∠BEF=∠EFC﹣∠EBC=2∠ADB﹣∠ADB=∠ADB=∠EBF,BF=EF=m,BC=BF+FC=m+n,再由△EBC∽△ADB,得出![]() =
=![]() =
=![]() ,代入数值即可得出结果;
,代入数值即可得出结果;
(3)由折叠性质知A′B=AB=n,∠A′BE=∠ABE,由△A′EB∽△BEC,得出![]() =
=![]() =
=![]() ,代入数值即可得出结果.
,代入数值即可得出结果.
解:(1)∠BCE=∠ABD,理由如下:
∵AD∥BC,
∴∠DBC=∠ADB,
∵DB=DC,
∴∠DCB=∠DBC=∠ADB,
∵DC=EC,
∴∠CDE=∠CED=∠DBC+∠BCE=∠ADB+∠BCE,
∵∠DBC+∠DCB+∠CDB=180°,即∠ADB+∠ADB+(∠ADB+∠BCE)=3∠ADB+∠BCE=180°,
又∵∠A+∠ABD+∠ADB=180°,∠A=2∠ADB,
∴3∠ADB+∠ABD=180°,
∴∠BCE=∠ABD;
(2)在BC上取一点F,使CF=AB=n,连接EF,如图1所示:
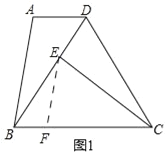
由(1)知:∠ABD=∠FCE,
在△ABD和△FCE中,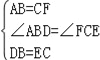 ,
,
∴△ABD≌△FCE(SAS),
∴∠EFC=∠DAB=2∠ADB,∠FEC=∠ADB,EF=AD=m,
∴∠BEF=∠EFC﹣∠EBC=2∠ADB﹣∠ADB=∠ADB=∠EBF,
∴BF=EF=m,BC=BF+FC=m+n,
∵∠EBC=∠ADB,∠BCE=∠DBA,
∴△EBC∽△ADB,
∴![]() =
=![]() =
=![]() ,即:
,即:![]() =
=![]() =
=![]() ,
,
∴DB=![]() ,
,
∴BE=![]() ;
;
(3)∵将△ABD沿BD翻折,得到△A′BD,点A′恰好落在EC上,
∴A′B=AB=n,∠A′BE=∠ABE,
由(1)知:∠ABE=∠BCE,
∴∠A′BE=∠BCE,
∵∠A′EB=∠BEC,
∴△A′EB∽△BEC,
∴![]() =
=![]() =
=![]() ,即:
,即:![]() =
=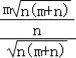 ,
,
整理得:m2+mn﹣n2=0,即(![]() )2+
)2+![]() ﹣1=0,
﹣1=0,
解得:![]() =
=![]() (负值舍去),
(负值舍去),
∴![]() =
=![]() .
.
“点睛”本题主要考查了平行线的性质、等腰三角形的性质、三角形内角和定理、全等三角形的判定与性质、折叠的性质、相似三角形的判定与性质、解一元二次方程等知识;熟练掌握相似三角形的判定与性质是解决问题的关键.


科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.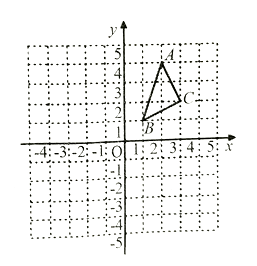
①作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;②在y轴上找点D,使得AD+BD最小,作出点D并写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程,然后回答问题.
计算: ![]() ÷
÷ ![]() ·(9-x2).
·(9-x2).
解:原式= ![]() ÷
÷ ![]() ·(3-x)(3+x) 第一步
·(3-x)(3+x) 第一步
= ![]() ·
· ![]() ·(3-x)(3+x) 第二步
·(3-x)(3+x) 第二步
=1. 第三步
(1)上述计算过程中,第一步使用的公式用字母表示为;
(2)第二步使用的运算法则用字母表示为;
(3)由第二步到第三步进行了分式的;
(4)以上三步中,第步出现错误,正确的化简结果是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( ) 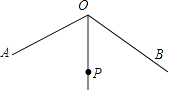
A.1个
B.2个
C.3个
D.3个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边三角形ABC中,点D在AB上(点D与点A,B不重合),DE⊥BC,垂足为E,点P在BC上,且DP∥AC,△B′DE′与△BDE关于DP对称.设BE=x,△B′DE′与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x<![]() ,
, ![]() ≤x<m与m≤x<n时,函数的解析式不同).
≤x<m与m≤x<n时,函数的解析式不同).
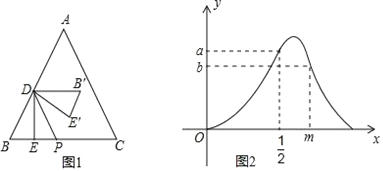
(1)填空:等边三角形ABC的边长为_____,图2中a的值为_____;
(2)求S关于x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华和小丽两人玩游戏,她们准备了A、B两个分别被平均分成三个、四个扇形的转盘.游戏规则:小华转动A盘、小丽转动B盘.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.两个转盘停止后指针所指区域内的数字之和小于6,小华获胜.指针所指区域内的数字之和大于6,小丽获胜.
(1)用树状图或列表法求小华、小丽获胜的概率;
(2)这个游戏规则对双方公平吗?请判断并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com