
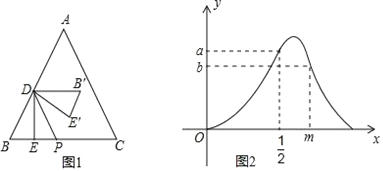
【题目】如图1,等边三角形ABC中,点D在AB上(点D与点A,B不重合),DE⊥BC,垂足为E,点P在BC上,且DP∥AC,△B′DE′与△BDE关于DP对称.设BE=x,△B′DE′与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x<![]() ,
, ![]() ≤x<m与m≤x<n时,函数的解析式不同).
≤x<m与m≤x<n时,函数的解析式不同).
(1)填空:等边三角形ABC的边长为_____,图2中a的值为_____;
(2)求S关于x的函数关系式,并直接写出x的取值范围.
【答案】 2, ![]() ; S=
; S=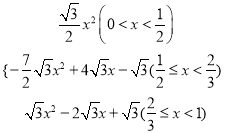
【解析】(1)先根据图象得到当x=BE=![]() 时,点B'在AC上,进而得出△ADB'是等边三角形,根据AD=DB'=DB=1,可得等边三角形ABC的边长为2,再根据S△DB'E'=S△DBE=
时,点B'在AC上,进而得出△ADB'是等边三角形,根据AD=DB'=DB=1,可得等边三角形ABC的边长为2,再根据S△DB'E'=S△DBE=![]() ,可得a的值;
,可得a的值;
(2)分三种情况讨论:当0<x<![]() 时,当
时,当![]() ≤x<
≤x<![]() 时,当
时,当![]() ≤x<1时,分别根据△B′DE′与△ABC重叠部分的形状,运用图形面积的和差关系得到S的表达式.
≤x<1时,分别根据△B′DE′与△ABC重叠部分的形状,运用图形面积的和差关系得到S的表达式.
解:(1)如图甲,
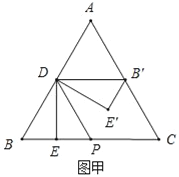
当x=BE=![]() 时,点B'在AC上,
时,点B'在AC上,
∵DE⊥BC,
∴∠BDE=30°,
∴BD=2BE=1,DE=![]() ,
,
又∵△B′DE′与△BDE关于DP对称,DP∥AC,
∴DB'=DB=1,且∠BDB'=60°×2=120°,
∴DB'∥BC,
∴△ADB'是等边三角形,
∴AD=DB'=DB=1,
∴AB=2,即等边三角形ABC的边长为2,
∵S△DB'E'=S△DBE=![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴a=![]() ,
,
故答案为:2,![]() ;
;
(2)当0<x<![]() 时,如图1,
时,如图1,
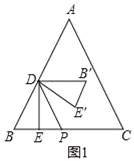
∵△ABC是等边三角形,DE⊥BC,
∴∠A=∠B=60°,∠BDE=30°,
∵△B′DE′与△BDE关于DP对称,
∴S=S△DB'E'=S△DBE=![]() BE×DE=
BE×DE=![]() x
x![]() x=
x=![]() x2;
x2;
当x=m时,点E'在AC上,此时,BE=AD=![]() AB=
AB=![]() ,即m=
,即m=![]() ,
,
当![]() ≤x<
≤x<![]() 时,如图2,
时,如图2,
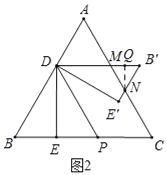
设B'D,B'E'分别与AC交于点M,N,
∵DP∥AC,
∴∠B'MN=∠DMA=∠MDP,∠BDP=∠A,
∵△B′DE′与△BDE关于DP对称,
∴∠MDP=∠BDP=∠A=60°,∠B'=∠B=60°,
∴∠B'MN=∠DMA=60°,
∴∠B'NM=60°=∠B'MN=∠B',∠ADM=60°=∠DMA=∠A,
∴△B'MN和△ADM都是等边三角形,
作NQ⊥B'M于Q,则NQ=![]() B'N,
B'N,
∵B'M=B'D﹣DM=BD﹣AD=2x﹣(2﹣2x)=4x﹣2,
∴S=S四边形DE'NM
=S△B'DE'﹣S△B'MN
=S△BDE﹣S△B'MN
=![]() x2﹣
x2﹣![]() (4x﹣2)
(4x﹣2)![]() (4x﹣2)
(4x﹣2)
=﹣![]() x2+4
x2+4![]() x﹣
x﹣![]() ;
;
当点D与点A重合时,x=BE=![]() BC=1,即n=1,
BC=1,即n=1,
当![]() ≤x<1时,如图3,
≤x<1时,如图3,
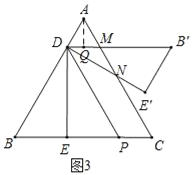
设B'D,DE'与AC分别交于点M,N,作AQ⊥DM于Q,
∵∠B'DE'=∠BDE=30°,∠ADM=60°,
∴∠ADN=90°,
∴S=S△MND
=S△ADN﹣S△ADM
=![]() (2﹣2x)
(2﹣2x)![]() (2﹣2x)﹣
(2﹣2x)﹣![]() (2﹣2x)
(2﹣2x)![]() (2﹣2x)
(2﹣2x)
=![]() x2﹣2
x2﹣2![]() x+
x+![]() .
.
综上所述,S关于x的函数关系式为:S=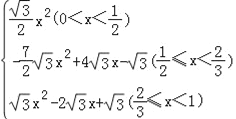


科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今社会手机越来越普及,有很多人开始过份依赖手机,一天中使用手机时间过长而形成了“手机瘾”.为了解我校初三年级学生的手机使用情况,学生会随机调查了部分学生的手机使用时间,将调查结果分成五类:A、基本不用;B、平均一天使用1~2小时;C、平均一天使用2~4小时;D、平均一天使用4~6小时;E、平均一天使用超过6小时.并用得到的数据绘制成了如下两幅不完整的统计图(图1、2),请根据相关信息,解答下列问题:

(1)将上面的条形统计图补充完整;
(2)若一天中手机使用时间超过6小时,则患有严重的“手机瘾”.我校初三年级共有1490人,试估计我校初三年级中约有多少人患有严重的“手机瘾”;
(3)在被调查的基本不用手机的4位同学中有2男2女,现要从中随机再抽两名同学去参加座谈,请你用列表法或树状图方法求出所选两位同学恰好是一名男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面的结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,其中结论正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AD∥BC,DB=DC=EC,∠A=2∠ADB,AD=m,AB=n.
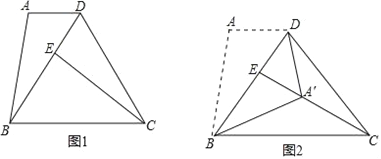
(1)在图1中找出与∠ABD相等的角,并加以证明;
(2)求BE的长;
(3)将△ABD沿BD翻折,得到△A′BD.若点A′恰好落在EC上(如图2),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作业时间是中小学教育质量综合评价指标的考查要点之一,腾飞学习小组五个同学每天课外作业时间分别是(单位:分钟):60,80,75,45,120.这组数据的中位数是( )
A.45
B.75
C.80
D.60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆的游泳池长50米,甲、乙二人分别在游泳池相对的A、B两边同时向另一边游去,其中s表示与A边的距离,t表示游泳时间,如图,l1 , l2分别表示甲、乙两人的s与t的关系.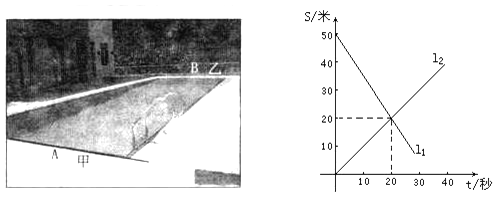
(1)l1表示谁到A边的距离s与游泳时间t的关系;
(2)甲、乙哪个速度快?
(3)游泳多长时间,两人相遇?
(4)t=30秒时,两人相距多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com