
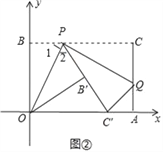
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是_____.

【答案】![]() 或
或![]()
【解析】∵把△OPB沿OP折叠,使点C落在点C′处,
∴BP=PB′,OB=OB′=6,∠A=∠OB′P=90°,
∵把△CPQ沿PQ折叠,使点D落在直线OA上的点C′处,
∴CP=C′P,CQ=C′Q,∠PC′Q=∠C=90°,
设BP=B′P=x,则PC=PC′=11﹣x,
∵BC∥AC,
∴∠1=∠EPOA,
∵∠1=∠2,
∴∠2=∠C′OP,
∴OC′=PC′=11﹣x,
∴B′C′=11﹣2x,
在Rt△OB′C′中,
∵OC′2=OB′2+B′C′2,
∴62+(11﹣2x)2=(11﹣x)2,
解得x=![]() ,
,
∴AE=![]() 或
或![]() .
.
故答案为![]() 或
或![]() .
.
点睛:本题主要考查了图形的折叠问题,矩形的性质,相似三角形的判定以及运用数形结合思想列方程的综合运用,运用相似的性质列比例式得出方程求出BP是解决问题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.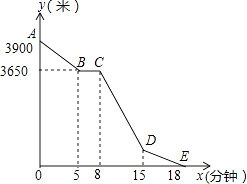
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边三角形ABC中,点D在AB上(点D与点A,B不重合),DE⊥BC,垂足为E,点P在BC上,且DP∥AC,△B′DE′与△BDE关于DP对称.设BE=x,△B′DE′与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x<![]() ,
, ![]() ≤x<m与m≤x<n时,函数的解析式不同).
≤x<m与m≤x<n时,函数的解析式不同).
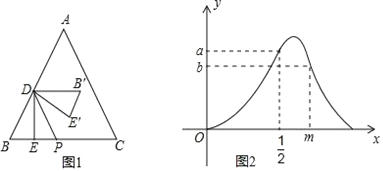
(1)填空:等边三角形ABC的边长为_____,图2中a的值为_____;
(2)求S关于x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com