
����Ŀ����������ֻ�Խ��Խ�ռ����кܶ��˿�ʼ���������ֻ���һ����ʹ���ֻ�ʱ��������γ��ˡ��ֻ���Ϊ�˽���У�����꼶ѧ�����ֻ�ʹ�������ѧ������������˲���ѧ�����ֻ�ʹ��ʱ�䣬���������ֳ����ࣺA���������ã�B��ƽ��һ��ʹ��1��2Сʱ��C��ƽ��һ��ʹ��2��4Сʱ��D��ƽ��һ��ʹ��4��6Сʱ��E��ƽ��һ��ʹ�ó���6Сʱ�����õõ������ݻ��Ƴ�������������������ͳ��ͼ��ͼ1��2��������������Ϣ������������⣺

��1�������������ͳ��ͼ����������
��2����һ�����ֻ�ʹ��ʱ�䳬��6Сʱ���������صġ��ֻ�����У�����꼶����1490�ˣ��Թ�����У�����꼶��Լ�ж����˻������صġ��ֻ���
��3���ڱ�����Ļ��������ֻ���4λͬѧ����2��2Ů����Ҫ��������ٳ�����ͬѧȥ�μ���̸���������б�������״ͼ���������ѡ��λͬѧǡ����һ����ͬѧ��һλŮͬѧ�ĸ��ʣ�
���𰸡�(1)����������2��149�ˣ���3��![]() .
.
�������������������1������A��������4��ռ8%���ó���������������������Ƶ�ʡ�Ƶ������ռ�İٷֱ�֮��Ĺ�ϵ����������𰸣��Ӷ���ȫͳ��ͼ��
(2)��ͼ֪���������ص����ֻ��������ռ�ٷֱ���10%������1490������1490��10%=149�ˣ�
��3�����������Ȼ���״ͼ���������еȿ��ܵij��ֽ����Ȼ����ݸ��ʹ�ʽ����𰸼��ɣ�
���������
��1��4��8%=50���ˣ�����BΪ50-4-20-9-5=12����������ͳ��ͼBΪ12.
��2��1490��10%=149���ˣ������Ի������ص����ֻ��������149��
��3�������
��1 | ��2 | Ů1 | Ů2 | |
��1 | ����1����2�� | ����1��Ů1�� | ����1��Ů2�� | |
��2 | ����1����2�� | ����2��Ů1�� | ����2��Ů2�� | |
Ů1 | ����1��Ů1�� | ����2��Ů1�� | ��Ů1��Ů2�� | |
Ů2 | ����1��Ů2�� | ����2��Ů2�� | ��Ů1��Ů2�� |
����12��ѡ��������һ��һŮ����8�֣����ԣ�ѡ����ǡ����һ��һŮ�ĸ�����:P=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������߶��ܹ��������ε��ǣ� ��
A. 1��2��3B. 3��4��5C. 3��6��9,D. 3��7��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A������Ϊ(1,3��a)������A��x��ľ�����3 ,��a=( )
A. 6B. 0C. ��6D. 0��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��A��B��C�����ڸ���ϣ�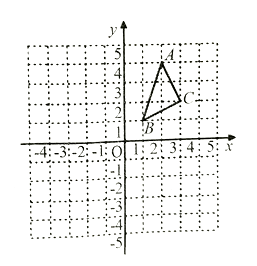
��������ABC����x��ԳƵġ�A1B1C1 �� ��д����C1�����ꣻ����y�����ҵ�D��ʹ��AD+BD��С��������D��д����D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A����Ϊ(6��0)����B��y����������ϣ��� ![]() =24 ��
=24 ��
��1�����B���ꣻ
��2������P��B������y�Ḻ���᷽���˶����ٶ�ÿ��2����λ���˶�ʱ��t�룬��AOP�����ΪS����S��t�Ĺ�ϵʽ����ֱ��д��t��ȡֵ��Χ��
��3����(2)�������£���S��AOP��S��ABP=1:3����S��AOP+S��ABP=S��AOB�����߶�AB�Ĵ�ֱƽ�������Ƿ���ڵ�Q��ʹ�á�AOQ��������BPQ�������ȣ������ڣ����Q�����ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����н������,Ȼ��ش�����.
����: ![]() ��
�� ![]() ��(9-x2).
��(9-x2).
��:ԭʽ= ![]() ��
�� ![]() ��(3-x)(3+x) ��һ��
��(3-x)(3+x) ��һ��
= ![]() ��
�� ![]() ��(3-x)(3+x) �ڶ���
��(3-x)(3+x) �ڶ���
=1. ������
��1���������������,��һ��ʹ�õĹ�ʽ����ĸ��ʾΪ;
��2���ڶ���ʹ�õ����㷨������ĸ��ʾΪ;
��3���ɵڶ����������������˷�ʽ��;
��4������������,�������ִ���,��ȷ�Ļ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ȱ�������ABC�У���D��AB�ϣ���D���A��B���غϣ���DE��BC������ΪE����P��BC�ϣ���DP��AC����B��DE�����BDE����DP�Գƣ���BE=x����B��DE�����ABC�ص����ֵ����ΪS��S����x�ĺ���ͼ����ͼ2��ʾ������0��x��![]() ��
�� ![]() ��x��m��m��x��nʱ�������Ľ���ʽ��ͬ����
��x��m��m��x��nʱ�������Ľ���ʽ��ͬ����
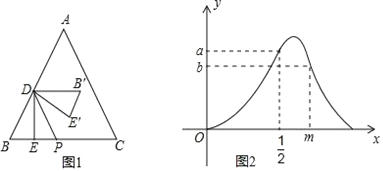
��1����գ��ȱ�������ABC�ı߳�Ϊ_____��ͼ2��a��ֵΪ_____��
��2����S����x�ĺ�����ϵʽ����ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2x+1��x+2=1����x��ֵ�ǣ�������
A.0
B.��2
C.��2��0
D.��2��0����1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com