
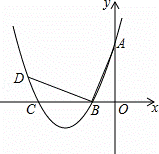
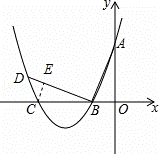
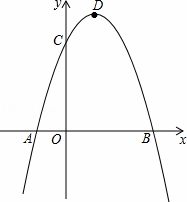
如图,在平面直角坐标系中.顶点为(﹣4,﹣1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
(1)求此抛物线的解析式;
(2)已知点P是抛物线上位于B,C两点之间的一个动点,问:当点P运动到什么位置时,四边形ABPC的面积最大?并求出此时四边形ABPC的面积.
(3)过点B作AB的垂线交抛物线于点D,是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆?若存在,求出圆的半径;若不存在,请说明理由.
解:(1)根据题意,可设抛物线的解析式为y=a(x+4)2﹣1,
把点A(0,3)代入得:3=16a﹣1,
解得a=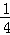 ,
,
所以此抛物线的解析式为y=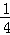 (x+4)2﹣1;
(x+4)2﹣1;
(2)令y=0,则0=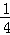 (x+4)2﹣1;
(x+4)2﹣1;
解得x1=﹣2,x2=﹣6,
∴B(﹣2,0),C(﹣6,0),
∴BC=4,
∵S四边形ABPC=S△ABC+S△PBC,S△ABC=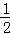 BC•OA=
BC•OA= ×4×3=6,
×4×3=6,
∴要使四边形ABPC的面积最大,则△PBC的面积最大,
∴当P点移动到抛物线的顶点是△PBC的面积最大,
∴四边形ABPC的面积的最大值为:S△ABC+S△PBC=6+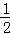 ×4×1=6+2=8;
×4×1=6+2=8;
(3)如图,设⊙C与BD相切于点E,连接CE,则∠BEC=∠AOB=90°.
∵A(0,3)、B(﹣2,0)、C(﹣6,0),
∴OA=3,OB=2,OC=6,BC=4;
∴AB=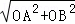 =
=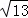 ,
,
∵AB⊥BD,
∴∠ABC=∠EBC+90°=∠OAB+90°,
∴∠EBC=∠OAB,
∴△OAB∽△EBC,
∴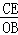 =
=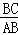 ,即
,即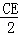 =
=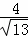
∴EC=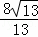 .
.
设抛物线对称轴交x轴于F.
∵抛物线的对称轴x=﹣4,
∴CF=2≠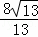 ,
,
∴不存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
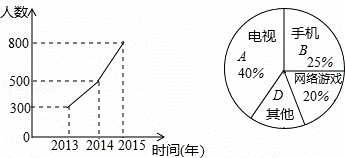
现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了解学生的视力变化情况,从全市九年级随机抽取了1500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
解答下列问题:
(1)图中D所在扇形的圆心角度数为 ;
(2)若2015年全市共有30000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
查看答案和解析>>
科目:初中数学 来源: 题型:
湘西土家族苗族自治州6月2日至6月8日最高气温(℃)统计如下表:
| 日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 |
| 最高气温℃ | 28 | 25 | 25 | 30 | 32 | 28 | 27 |
则这七天最高气温的中位数为( )
A.25℃ B. 27℃ C. 28℃ D. 30℃
查看答案和解析>>
科目:初中数学 来源: 题型:
下列乘法中,能运用完全平方公式进行运算的是( )
A.(x+a)(x-a) B.(b+m)(m-b) C.(-x-b)(x-b) D.(a+b)(-a-b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com