
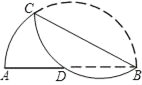
【题目】如图,在以AB为直径的半圆中,将弧BC沿弦BC折叠交AB于点D,若AD=5,DB=7.
(1)求BC的长;
(2)求圆心到BC的距离.
【答案】(1)![]() ;(2)圆心到BC的距离为
;(2)圆心到BC的距离为![]() .
.
【解析】(1)根据折叠的性质知:![]() ;若连接CD、AC,则∠DBC+∠BCD=∠CAD,即∠CAD=∠CDA;过C作AB的垂线,设垂足为E,则DE=
;若连接CD、AC,则∠DBC+∠BCD=∠CAD,即∠CAD=∠CDA;过C作AB的垂线,设垂足为E,则DE=![]() AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.
AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.
(2)设圆心到BC的距离为h,利用勾股定理解答即可.
(1)连接CA、CD;
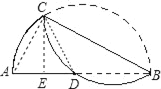
根据折叠的性质,得:![]() ;
;
∴∠CAB=∠CBD+∠BCD;
∵∠CDA=∠CBD+∠BCD(三角形的一个外角等于和它不相邻的两个内角的和),
∴∠CAD=∠CDA,即△CAD是等腰三角形;
过C作CE⊥AB于E,则AE=DE=2.5;
∴BE=BD+DE=9.5;
在Rt△ACB中,CE⊥AB,根据射影定理,得:
BC2=BEAB=9.5×12=114;
故BC=![]() .
.
(2)设圆心到BC的距离为h,圆的半径为r=6,
由(1)知,Rt△ECB中,BE=9.5,BC=![]() ,
,
∴![]() ,
,
∵sin=![]() ,
,
∴h=![]() ,
,
故圆心到BC的距离为![]() .
.


科目:初中数学 来源: 题型:
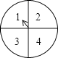
【题目】如图,转盘被划分成![]() 个相同的小扇形,并分别标上数字
个相同的小扇形,并分别标上数字![]() ,
,![]() ,
,![]() ,
,![]() ,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中
,分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中![]() 点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点
点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,认为指向左侧扇形的数字,则点![]() 落在直线
落在直线![]() 的下方的概率为( )
的下方的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题:如图1,在四边形ABCD中,∠B=∠C=90°,E是BC的中点,AE、DE分别平分∠DAB、∠CDA.求证:AD=AB+CD.
小明经探究发现,在AD上截取AF=AB,连接EF(如图2),从而可证△AEF≌△AEB,使问题得到解决.

(1)请你按照小明的探究思路,完成他的证明过程;
参考小明思考问题的方法,解决下面的问题:
(2)如图3,△ABC是等腰直角三角形,∠A=90°,点D为边AC上任意一点(不与点A、B重合),以BD为腰作等腰直角△BDE,∠DBE=90°.过点E作BE⊥EG交BA的延长线于点G,过点D作DF⊥BD,交BC于点F,连接FG,猜想EG、DF、FG之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AC = BC.分别过A,B点作互相平行的直线AM和BN.过点C的直线分别交直线AM,BN于点D,E。

(1)如图1.若CD= CE .求∠ABE的大小:
(2)如图2.∠ABC= ∠DEB= 60°.求证:AD+DC = BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店按进货价每件6元购进一批货,零售价为8元时,可以卖出100件,如果零售价高于8元,那么一件也卖不出去,零售价从8元每降低0.1元,可以多卖出10件.设零售价定为x元(6≤x≤8).
(1)这时比零售为8元可以多卖出几件?
(2)这时可以卖出多少件?
(3)这时所获利润y(元)与零售价x(元)的关系式怎样?
(4)为零售价定为多少时,所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是等腰梯形,OA∥BC,A的坐标(4,0),B的坐标(3,2),点M从O点以每秒3个单位的速度向终点A运动;同时点N从B点出发以每秒1个单位的速度向终点C运动(M到达点A后停止,点N继续运动到C点停止),过点N作NP⊥OA于P点,连接AC交NP于Q,连接MQ,如动点N运动时间为t秒.
(1)求直线AC的解析式;
(2)当t取何值时?△AMQ的面积最大,并求此时△AMQ面积的最大值;
(3)是否存在t的值,使△PQM与△PQA相似?若存在,求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥享有“中国淡水龙虾之都”的美称.甲乙两家小龙虾美食店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲乙两家店都让利酬宾,在人数不超过20人的前提下,付款金额y甲,y乙(单位元)与人数之间的函数关系如图所示.

(1)直接写出y甲,y乙关于x的函数关系式.
(2)小王公司想在“龙虾节”期间组织团建,在甲乙两家店就餐,如何选择甲乙两家美食店吃小龙虾更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:如图是华师版八年级上册数学教材第94页的部分内容.2.线段垂直平分线.我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴,如图,直线MN是线段AB的垂直平分线,P是MN上任一点,连结PA、PB,将线段AB沿直线MN对称,我们发现PA与PB完全重合,由此即有:线段垂直平分线的性质定理 线段垂直平分线上的点到线段的距离相等.已知:如图,MN⊥AB,垂足为点C,AC=BC,点P是直线MN上的任意一点.求证:PA=PB.图中有两个直角三角形APC和BPC,只要证明这两个三角形全等,便可证明PA=PB.

定理证明:请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.
定理应用:
(1)如图②,在△ABC中,直线m、n分别是边BC、AC的垂直平分线,直线m、n的交点为O.过点O作OH⊥AB于点H.求证:AH=BH.
(2)如图③,在△ABC中,AB=BC,边AB的垂直平分线l交AC于点D,边BC的垂直平分线k交AC于点E.若∠ABC=120°,AC=15,则DE的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com