
【题目】阅读下面材料:小明遇到这样一个问题:如图1,在四边形ABCD中,∠B=∠C=90°,E是BC的中点,AE、DE分别平分∠DAB、∠CDA.求证:AD=AB+CD.
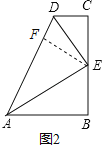
小明经探究发现,在AD上截取AF=AB,连接EF(如图2),从而可证△AEF≌△AEB,使问题得到解决.

(1)请你按照小明的探究思路,完成他的证明过程;
参考小明思考问题的方法,解决下面的问题:
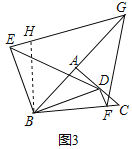
(2)如图3,△ABC是等腰直角三角形,∠A=90°,点D为边AC上任意一点(不与点A、B重合),以BD为腰作等腰直角△BDE,∠DBE=90°.过点E作BE⊥EG交BA的延长线于点G,过点D作DF⊥BD,交BC于点F,连接FG,猜想EG、DF、FG之间的数量关系,并证明.
【答案】(1)证明见解析;(2)猜想EG=DF+FG,理由见解析.
【解析】
(1)如图2,作辅助线EF,使AB=AF,构建全等三角形,△AEF≌△AEB,△DEF≌△DEC,得出FD=CD,从而得出结论;(2)猜想EG=DF+FG,在EG上截取EH=DF,连接BH,根据已知条件证明 △BEH≌△BDF,找出∠ABH=45°,再证明△BGH≌△BGF,即可得出结论.
(1)证明;在AD上截取AF=AB,连接EF,如图2所示:
∵AE、DE分别平分∠DAB、∠CDA,
∴∠BAE=∠FAE,∠CDE=∠FDE,
在△AEF和△AEB中,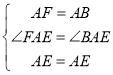 ,
,
∴△AEF≌△AEB(SAS),
∴∠AFE=∠B=90°,
∴∠DFE=90°,
在△DEF和△DEC中,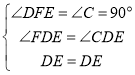 ,
,
∴△DEF≌△DEC(AAS),
∴FD=CD,
∵AD=AF+FD,
∴AD=AB+CD;
(2)解:猜想EG=DF+FG,理由如下:
在EG上截取EH=DF,连接BH,如图3所示:
∵BE⊥EG,DF⊥BD,
∴∠BEH=∠BDF=90°,
∵△BDE是等腰直角三角形,
∴BE=BD,∠EBD=90°,
在△BEH和△BDF中,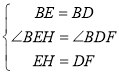 ,
,
∴△BEH≌△BDF(SAS),
∴BH=BF,∠EBH=∠DBF,
∴∠EBH+∠HBD=∠DBF+∠HBD,
∴∠EBH=∠HBC=90°,
∵△ABC是等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠ABH=45°,
在△BGH和△BGF中,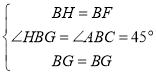 ,
,
∴△BGH≌△BGF(SAS),
∴GH=GF,
∵EG=EH+GH,
∴EG=DF+FG.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是60%”表示明天有60%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “某篮球运动员投篮的命中率大约是82.3%”表示投篮1次,命中的可能性较大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有10名工作人员他们的月工资情况如表(其中x为未知数),他们的月平均工资是2.3万元,根据表中信息计算该公司工作人员的月工资的中位数和众数分别是( )
职位 | 经理 | 副经理 | A职员 | B职员 | C职员 |
人数 | 1 | 2 | 2 | 4 | 1 |
月工资(万元/人) | 5 | 3 | 2 | x | 0.8 |
A. 2,4 B. 1.9,1.8 C. 2,1.8 D. 1.8,1.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,AC=25cm,BC=15cm
(1)设点P在AB上,若∠PAC =∠PCA.求AP的长;
(2)设点M在AC上.若△MBC为等腰三角形,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx过点A(1,4)、B(﹣3,0),过点A作直线AC∥x轴,交抛物线于另一点C,在x轴上有一点D(4,0),连接CD.

(1)求抛物线的表达式;
(2)若在抛物线上存在点Q,使得CD平分∠ACQ,请求出点Q的坐标;
(3)在直线CD的下方的抛物线上取一点N,过点N作NG∥y轴交CD于点G,以NG为直径画圆在直线CD上截得弦GH,问弦GH的最大值是多少?
(4)一动点P从C点出发,以每秒1个单位长度的速度沿C﹣A﹣D运动,在线段CD上还有一动点M,问是否存在某一时刻使PM+AM=4?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点A(0,3)且与两坐标轴所围成的三角形的面积为3,则这个一次函数的表达式为( )
A. y=1.5x+3 B. y=-1.5x+3 C. y=1.5x+3或y=-1.5x+3 D. 无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com