已知:四边形ABCD中,AD∥BC,AB=AD=DC,∠BAD=∠ADC,点E在CD边上运动(点E与点C、D两点不重合),△AEP为,直角三角形,∠AEP=90°,∠P=30°,过点E作EM∥BC交AF于点M.
(1)若∠BAD=120°(如图1),求证:BF+DE=EM;
(2)若∠BAD=90°(如图2),则线段BF、DE、EM的数量关系为______
【答案】
分析:(1)延长FB到N,使BN=ED,连接AN、EF,通过求证△ADE≌△ABN,推出AN=AE,∠DAE=∠BAN,根据∠AD=120°,∠EAF=60°,推出∠NAF=∠EAF,继而推出△ANF≌△AEF,求得NF=EF,∠AFN=∠AFE后,结合ME∥BC,推出∠AFB=∠EMF=∠AFE,即可推出ME=EF,可得BF+DE=EM.
(2)延长CB至N点,使BN=DE,根据题意即可推出△ABN≌△ADE,求得∠EAD=∠NAB,NF=DE+BF,AN=AE,求得∠BAN+∠BAF=30°,由∠P=30°,∠AEP=90°,得
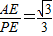
,∠BAN+∠BAF=30°,再由ME∥BC,推出∠NFA=∠FME,得△ANF∽△PEM,由AN=AE,即可推出
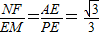
,通过计算可得BF+DE=
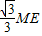
.
(3)过D点做DG∥AB交BC于G点,作EK⊥BC于K点,连接EF,由四边形ABGD为平行四边形,∠BAD=120°,∠ABC=∠C=60°,推出△DGC为等边三角形,设AD=3x,BF=2x,根据BF+DE=EM,EM=7,得,DE=7-2x,EC=5x-7,EF=EM=7,继而推出BC=6x,FC=4x,求出EK=
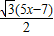
,FK=4x-
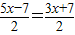
后,根据勾股定理,即可求出x的值,继而求得EC的长度.
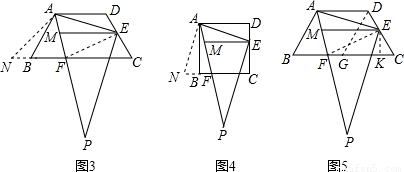
解答:解:(1)如图3,延长FB到N,使BN=ED,连接AN、EF,
∵∠AEP=90°,∠P=30°,
∴∠PAE=60°,
∵AB=AD,AD∥BC,
∴∠BAD=∠ABN=∠D,
∵在△ADE和△ABN中,
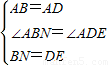
,
∴△ADE≌△ABN(SAS),
∴AN=AE,∠DAE=∠BAN,
∵∠BAD=120°,∠PAE=60°,
∴∠NAF=∠EAF,
∵在△ANF和△AEF中,
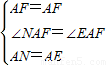
,
∴△ANF≌△AEF(SAS),
∴NF=EF,∠AFN=∠AFE,
∵ME∥BC,
∴∠AFB=∠EMF=∠AFE,
∴ME=EF,
∴BF+DE=EM,
(2)如图4,延长CB至N点,使BN=DE,
∵AB=AD=DC,∠BAD=∠ADC=90°,
∴四边形ABCD为正方形,
∵在△ABN和△ADE中,
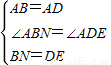
,
∴△ABN≌△ADE(SAS),
∴∠EAD=∠NAB,NF=DE+BF,AN=AE,
∵∠P=30°,∠AEP=90°,
∴∠PAE=60°,
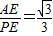
,
∴∠EAD+∠BAF=30°,
∴∠BAN+∠BAF=30°,
∠NAP=∠P,
∵ME∥BC,
∴∠NFA=∠FME,
∴△ANF∽△PEM,
∴
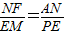
,
∵AN=AE,
∴
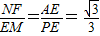
,
∴BF+DE=
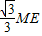
,
(3)过D点做DG∥AB交BC于G点,作EK⊥BC于K点,连接EF,
∵AD∥BC,
∴四边形ABGD为平行四边形,
∵∠BAD=120°,
∴∠ABC=∠C=60°,
∴△DGC为等边三角形,
设AD=3x,BF=2x,
∵BF+DE=EM,EM=7,
∴DE=7-2x,EC=5x-7,EF=EM=7,
∵AB=AD,四边形ABGD为平行四边形,
∴AD=BG,
∴BC=6x,FC=4x,
∵EK⊥BC,
∴EK=
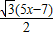
,FK=4x-
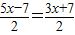
,
∵EF
2=FK
2+EK
2,
∴(
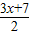
)
2+[
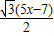
]
2=49,
解方程的:x=2,
∴EC=3.
 点评:
点评:本题主要考查全等三角形的判定与性质,相似三角形的判定与性质,平行线的判定与性质,勾股定理,特殊角的三角函数值等知识点,关键在于熟练的综合运用相关的性质定理,正确的做出辅助线,正确的求证相关的三角形全等,认真的进行计算.

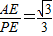 ,∠BAN+∠BAF=30°,再由ME∥BC,推出∠NFA=∠FME,得△ANF∽△PEM,由AN=AE,即可推出
,∠BAN+∠BAF=30°,再由ME∥BC,推出∠NFA=∠FME,得△ANF∽△PEM,由AN=AE,即可推出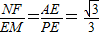 ,通过计算可得BF+DE=
,通过计算可得BF+DE=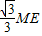 .
.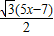 ,FK=4x-
,FK=4x-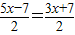 后,根据勾股定理,即可求出x的值,继而求得EC的长度.
后,根据勾股定理,即可求出x的值,继而求得EC的长度.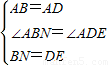 ,
,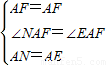 ,
,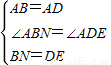 ,
,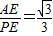 ,
,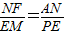 ,
,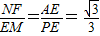 ,
,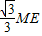 ,
,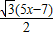 ,FK=4x-
,FK=4x-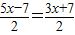 ,
,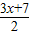 )2+[
)2+[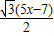 ]2=49,
]2=49,


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
 34、如图:在平行四边形ABCD中,∠B=30°,AE⊥BC于点E,AF⊥DC的延长线于点F,已知平行四边形ABCD的周长为40cm,且AE:AF=2:3.求平行四边形ABCD的面积.
34、如图:在平行四边形ABCD中,∠B=30°,AE⊥BC于点E,AF⊥DC的延长线于点F,已知平行四边形ABCD的周长为40cm,且AE:AF=2:3.求平行四边形ABCD的面积. 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD. 如图,已知平行四边形ABCD,E是边AB的中点,联结AC、DE交于点O.记向量
如图,已知平行四边形ABCD,E是边AB的中点,联结AC、DE交于点O.记向量