
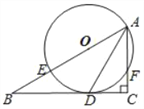
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OD,由 OD=OA,可得∠1=∠2,再由BC为⊙O的切线,根据切线的性质可得∠ODB=90°,已知∠C=90°,所以∠ODB=∠C,即可判定OD∥AC,根据平行线的性质可得∠3=∠2,所以∠1=∠3,即可判定AD是∠BAC的平分线;(2)连接DF,已知∠B=30°,可求得∠BAC=60°,再由AD是∠BAC的平分线,可得∠3=30°,已知BC是⊙O的切线,根据弦切角定理可得∠FDC=∠3=30°,所以CD=![]() CF=
CF=![]() ,同理可得AC=
,同理可得AC=![]() CD=3,所以AF=2,过O作OG⊥AF于G,由垂径定理可得GF=
CD=3,所以AF=2,过O作OG⊥AF于G,由垂径定理可得GF=![]() AF=1,四边形ODCG是矩形,所以CG=2,OG=CD=
AF=1,四边形ODCG是矩形,所以CG=2,OG=CD=![]() ,由勾股定理可得OC=
,由勾股定理可得OC=![]() .
.
试题解析:
(1)证明:连接OD,∴OD=OA,∴∠1=∠2,
∵BC为⊙O的切线,∴∠ODB=90°,∵∠C=90°,∴∠ODB=∠C,∴OD∥AC,
∴∠3=∠2,∴∠1=∠3,∴AD是∠BAC的平分线;
(2)解:连接DF,∵∠B=30°,∴∠BAC=60°,
∵AD是∠BAC的平分线,∴∠3=30°,∵BC是⊙O的切线,∴∠FDC=∠3=30°,
∴CD=![]() CF=
CF=![]() ,∴AC=
,∴AC=![]() CD=3,∴AF=2,
CD=3,∴AF=2,
过O作OG⊥AF于G,∴GF=AF=1,四边形ODCG是矩形,
∴CG=2,OG=CD=![]() ,∴OC=
,∴OC=![]() =
=![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】为了迎接第二届“环泉州湾国际自行车赛”的到来,泉州台商投资区需要制作宣传单.有两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而制版费900元则六折优惠.且甲乙两厂都规定:一次印刷数量至少是500份.
(1)若印刷数量为![]() 份(
份(![]() ,且
,且![]() 是整数),请你分别写出两个印刷厂收费的代数式;
是整数),请你分别写出两个印刷厂收费的代数式;
(2)如果比赛宣传单需要印刷1100份,应选择哪个厂家?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌专卖店对上个月销售的男运动鞋尺码统计如下:
码号(码) | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
销售量(双) | 6 | 8 | 14 | 20 | 17 | 3 | 1 |
这组统计数据中的众数是码.
查看答案和解析>>
科目:初中数学 来源: 题型:
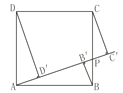
【题目】如图,正方形ABCD的边长为1,点P为BC上任意一点(可与点B或C重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最小值是( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com