
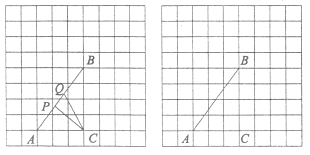
【题目】如图,在由边长都为1的小正方形组成的网格中,点![]() 均为格点,点
均为格点,点![]() 为线段
为线段![]() 上的动点,且满足
上的动点,且满足![]() .
.
(Ⅰ)当点Q为线段![]() 中点时
中点时![]() 的长度等于________.
的长度等于________.
(Ⅱ)当线段![]() 取得最小值时,请借助无刻度直尺在给定的网格中画出点Q,并简要说明你是怎么画出点Q的:_______.
取得最小值时,请借助无刻度直尺在给定的网格中画出点Q,并简要说明你是怎么画出点Q的:_______.
【答案】(Ⅰ)![]() (Ⅱ)取格点
(Ⅱ)取格点![]() ,连接
,连接![]() ,它们相交于点G,取格点
,它们相交于点G,取格点![]() .连接
.连接![]() ,它们相交于点M,连接
,它们相交于点M,连接![]() ,取格点
,取格点![]() .连接
.连接![]() 并延长,交
并延长,交![]() 于点T,连接
于点T,连接![]() ,交
,交![]() 于点Q,则点Q即为所求,见解析.
于点Q,则点Q即为所求,见解析.
【解析】
(Ⅰ)先根据勾股定理得出AB的长,再根据直角三角形斜边上的中线等于斜边的一半,即可求出![]() 的长度
的长度
(Ⅱ)取格点![]() ,连接
,连接![]() ,它们相交于点G,取格点
,它们相交于点G,取格点![]() .连接
.连接![]() ,它们相交于点M,连接
,它们相交于点M,连接![]() ,取格点
,取格点![]() .连接
.连接![]() 并延长,交
并延长,交![]() 于点T,连接
于点T,连接![]() ,交
,交![]() 于点Q,
于点Q,
解:(Ⅰ)在Rt![]() ,
,![]() ,
,
∴AB=![]() =5
=5
∵点Q为线段![]() 中点
中点
∴![]() ;
;
故答案为:![]()
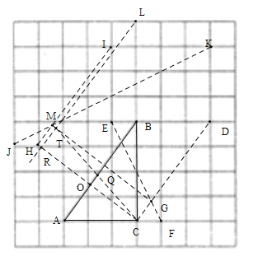
(Ⅱ)线段![]() 取得最小值时,点P,Q必在线段AB的高线的垂足的两侧,并关于垂足对称,即离垂足的距离为0.5.所以先找到点C关于AB的对称点,首先先找垂线,因为AB是3×4的格点矩形的对角线,所以只需过点C作3×4的格点矩形的对角线CH即可满足CH⊥AB垂足为O,下一步找距离相等.可找到D点,构成3×4的格点矩形的对角线CD,则有CD∥AB,且BD=3,同样找到格点N,L使其为3×4的格点矩形的对角线端点,且BN=3,则有LN与CD到AB的距离相等且平行,延长LN则与CH相交R,则交点即为C关于AB的对称点.现要保证OQ=0.5,则只需在LR上找到点T,CD上找到点G,使得RT=CG=1,则四边形RCGT为矩形.因为CD=5,则只需找到CD的五等分点,找到格点E,F,使CF=1,DE=4,且CF∥ED,则CD与EF的交点为G.因为在LR上找的点T不能直接找到,我们可以过点H作AB的平行线HI,并在HI上找到点M使得HM=1,则MG与LR 的交点即为T点,且OT=1.则易找到格点I使得HI∥AB,同E,F的找法,找到格点J,K,连接JK交HI 于点M ,则HM=1,连接MG交LR于点T,再连接TC与AB的交点为Q,则点Q即为所求.
取得最小值时,点P,Q必在线段AB的高线的垂足的两侧,并关于垂足对称,即离垂足的距离为0.5.所以先找到点C关于AB的对称点,首先先找垂线,因为AB是3×4的格点矩形的对角线,所以只需过点C作3×4的格点矩形的对角线CH即可满足CH⊥AB垂足为O,下一步找距离相等.可找到D点,构成3×4的格点矩形的对角线CD,则有CD∥AB,且BD=3,同样找到格点N,L使其为3×4的格点矩形的对角线端点,且BN=3,则有LN与CD到AB的距离相等且平行,延长LN则与CH相交R,则交点即为C关于AB的对称点.现要保证OQ=0.5,则只需在LR上找到点T,CD上找到点G,使得RT=CG=1,则四边形RCGT为矩形.因为CD=5,则只需找到CD的五等分点,找到格点E,F,使CF=1,DE=4,且CF∥ED,则CD与EF的交点为G.因为在LR上找的点T不能直接找到,我们可以过点H作AB的平行线HI,并在HI上找到点M使得HM=1,则MG与LR 的交点即为T点,且OT=1.则易找到格点I使得HI∥AB,同E,F的找法,找到格点J,K,连接JK交HI 于点M ,则HM=1,连接MG交LR于点T,再连接TC与AB的交点为Q,则点Q即为所求.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
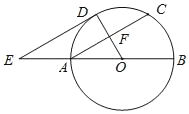
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接AD、CD、OC.填空
①当∠OAC的度数为 时,四边形AOCD为菱形;
②当OA=AE=2时,四边形ACDE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是五角星、六角星、七角星、八角星的图形;
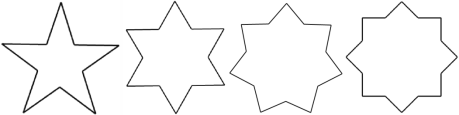
(1)请问其中是中心对称图形的是哪些?
(2)依次类推,36角星是不是中心对称图形?
(3)怎样判断一个n角星是否是中心对称图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2﹣2x+3.
(1)把函数关系式配成顶点式并求出图象的顶点坐标和对称轴.
(2)若图象与x轴交点为A.B,与y轴交点为C,求A、B、C三点的坐标;
(3)在图中画出图象.并求出△ABC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组销售额数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
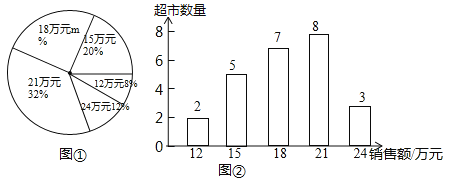
(Ⅰ)该商场服装部营业员的人数为_____________,图①中![]() 的值为____________;
的值为____________;
(Ⅱ)求统计的这组销售额数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,己知O为坐标原点,点![]() ,以点A为旋转中心,把
,以点A为旋转中心,把![]() 顺时针旋转,得
顺时针旋转,得![]() .
.

(Ⅰ)如图①,当旋转后满足![]() 轴时,求点C的坐标.
轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
(Ⅲ)在(Ⅱ)的条件下,边![]() 上的一点P旋转后的对应点为
上的一点P旋转后的对应点为![]() ,当
,当![]() 取得最小值时,求点P的坐标(直接写出结果即可)
取得最小值时,求点P的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
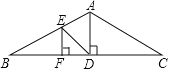
【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
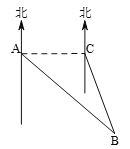
【题目】如图,小岛![]() 正好在深水港口
正好在深水港口![]() 的东南方向,一艘集装箱货船从港口
的东南方向,一艘集装箱货船从港口![]() 出发,沿正东方向以每小时30千米的速度行驶,40分钟后在
出发,沿正东方向以每小时30千米的速度行驶,40分钟后在![]() 处测得小岛
处测得小岛![]() 在它的南偏东
在它的南偏东![]() 方向,求小岛
方向,求小岛![]() 离深水港口
离深水港口![]() 的距离(精确到0.1千米).参考数据:
的距离(精确到0.1千米).参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com