Question

【题目】如图，△ABC中，AB=AC，点P是三角形右外一点，且∠APB=∠ABC．

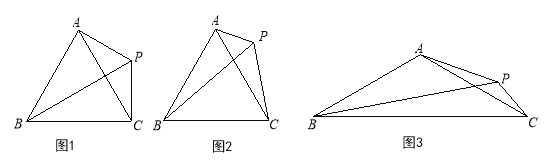
（1）如图1，若∠BAC=60°，点P恰巧在∠ABC的平分线上，PA=2，求PB的长；

（2）如图2，若∠BAC=60°，探究PA，PB，PC的数量关系，并证明；

（3）如图3，若∠BAC=120°，请直接写出PA，PB，PC的数量关系．

Answer 1

【答案】（1）、BP=4；（2）、PA+PC=PB，证明过程见解析；（3）、PA+PC=PB

【解析】

试题分析：（1）、根据题意得出△ABC为等边三角形，根据点P在∠ABC的平分线上，则∠ABP=30°，根据∠PAB=90°得出BP=2AP；（2）、在在BP上截取PD，使PD=PA，连结AD，证明△ABD和△ACP全等，从而得出PC=BD，得出所求的答案；（3）、根据同样的方法得出线段之间的关系.

试题解析：（1）、∵AB=AC，∠BAC=60°，

∴△ABC是等边三角形，∠APB=∠ABC，

∴∠APB=60°，

又∵点P恰巧在∠ABC的平分线上，

∴∠ABP=30°

∴∠PAB=90°．

∴BP=2AP，

∵AP=2，

∴BP=4．

（2）、结论：PA+PC=PB．

在BP上截取PD，使PD=PA，连结AD．

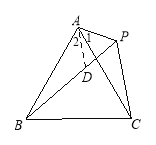
∵∠APB =60°，

∴△ADP是等边三角形，

∴∠DAP =60°，

∴∠1=∠2，PA=PD，

又∵AB=AC，

∴△ABD≌△ACP，

∴PC=BD，

∴PA+PC=PB．

（3）、结论：PA+PC=PB．