
 已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.
已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6. 分析 作QH⊥BC,交BC的延长线于H,易证Rt△ADP∽Rt△QHC.由DE=2PD,则BH即可.由图知,当PQ⊥AB时,PQ的长最小值即可求得.
解答  解:作QH⊥BC,交BC的延长线于H,
解:作QH⊥BC,交BC的延长线于H,
∵AB∥QH,
∴∠APD+∠DPQ=∠PQC+∠CQH.
∵以PE,PC 为边作?PCQE,
∴PE∥CQ,
∴∠DPQ=∠PQC,
∴∠APD=∠CQH,
∴Rt△ADP∽Rt△QHC.
∴$\frac{PD}{QC}$=$\frac{AP}{HQ}$,即$\frac{PD}{PE}$=$\frac{AD}{HC}$,
∵DE=2PD,
∴$\frac{PD}{3PD}$=$\frac{AD}{HC}$,
∵AD=1,
∴HC=2+1=3,
∵BC=3,
∴BH=3+2+1=6.
∴由图知,当PQ⊥AB时,PQ的长最小值为6.
故答案是:6.
点评 此题考查了相似三角形的判定与性质、直角梯形的性质、平行四边形的性质、矩形的性质,注意准确作出辅助线是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
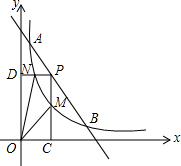 如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是$\frac{25}{2}$.
如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是$\frac{25}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
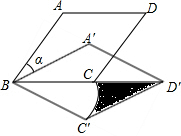 如图,在菱形ABCD中,AB=2$\sqrt{3}$,∠ABC=60°,把菱形ABCD绕点B顺时针旋转α得到菱形A′BC′D′,其中点D′落在BC的延长线上,点C的运动路径为$\widehat{CC′}$,则图中阴影部分的面积为3$\sqrt{3}$-π.
如图,在菱形ABCD中,AB=2$\sqrt{3}$,∠ABC=60°,把菱形ABCD绕点B顺时针旋转α得到菱形A′BC′D′,其中点D′落在BC的延长线上,点C的运动路径为$\widehat{CC′}$,则图中阴影部分的面积为3$\sqrt{3}$-π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
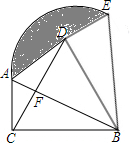 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则阴影部分的面积为$\frac{169π}{6}$-$\frac{169\sqrt{3}}{4}$..
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则阴影部分的面积为$\frac{169π}{6}$-$\frac{169\sqrt{3}}{4}$..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
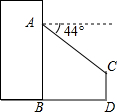 如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)
如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com