
 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.分析 (1)先证明四边形AMCN是平行四边形,再由翻折得AM=CM,则四边形AMCN是菱形.
(2)根据题意求出$\frac{MC}{DN}=\frac{3}{1}$,设MC=3λ;用λ来表示CD、AB的长,运用面积公式即可解决问题.
解答 证明:(1)如图,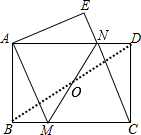
连接BD,则BD过点O,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴∠OBM=∠ODN,
在△OBM和△ODN中,
$\left\{\begin{array}{l}{∠OBM=∠ODN}\\{OB=OD}\\{∠BOM=∠ODN}\end{array}\right.$,
∴△OBM≌△ODN,
∴BM=DN;
∴AN=CM,
∴四边形AMCN是平行四边形,
由翻折得,AM=CM,
∴四边形AMCN是菱形.
(2):∵△CMN的面积与△CDN的面积比为3:1,
∴$\frac{\frac{1}{2}MC•DC}{\frac{1}{2}DN•DC}=\frac{3}{1}$,即$\frac{MC}{DN}=\frac{3}{1}$,
设MC=3λ,则DN=λ,AD=4λ,CN=3λ;
由勾股定理得:CD2=CN2-DN2=8λ2,
∴CD=2$\sqrt{2}$λ;同理可求AC=2$\sqrt{6}$λ;
由面积公式得:MC•CD=$\frac{1}{2}$AC•MN,
即3λ•2$\sqrt{2}$λ=$\frac{1}{2}$×2$\sqrt{6}$λ•MN,
∴MN=2$\sqrt{3}$λ,
∴$\frac{MN}{DN}=\frac{2\sqrt{3}λ}{λ}=2\sqrt{3}$.
点评 此题考查了矩形的性质、折叠的性质、菱形的判定,注意掌握辅助线的作法,灵活利用图形的性质解决问题.


科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:单选题
函数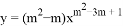 是反比例函数,则( )
是反比例函数,则( )
A. m≠0 B. m≠0且m≠1 C. m=2 D. m=1或2
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:判断题
在边长为1的正方形ABCD中,点E是射线BC上一动点,AE与BD相交于点M,AE或其延长线与DC或其延长线相交于点F,G是EF的中点,连结CG.
(1)如图1,当点E在BC边上时.求证:①△ABM≌△CBM;②CG⊥CM.
(2)如图2,当点E在BC的延长线上时,(1)中的结论②是否成立?请写出结论,不用证明.
(3)试问当点E运动到什么位置时,△MCE是等腰三角形?请说明理由.
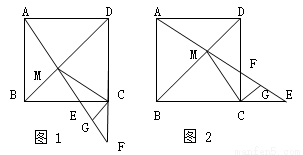
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:填空题
如图,在扇形OAB中,∠AOB=60°,扇形半径为r,点C在 ,CD⊥OA,垂足为D,当△OCD的面积最大时,
,CD⊥OA,垂足为D,当△OCD的面积最大时,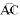 的长为____.
的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
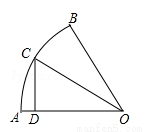
 如图,若AD、BE为△ABC的两条角平分线,I为内心,若C,D,I,E四点共圆,且DE=1,则ID=$\frac{\sqrt{3}}{3}$.
如图,若AD、BE为△ABC的两条角平分线,I为内心,若C,D,I,E四点共圆,且DE=1,则ID=$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
如图,O为原点,点A的坐标为(-1,2),将△ABO绕点O顺时针旋转90°后得到△CEO,则点A的对应点C的坐标为( )
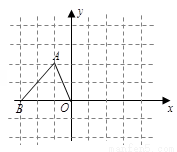
A. (1,2) B. (2,1) C. (-2,1) D. (-2,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com