
 如图,抛物线y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.分析 (1)利用坐标轴上点的特点求出A、B、C点的坐标,再用待定系数法求得直线BC的解析式;
(2)设点D的横坐标为m,则坐标为(m,$\frac{1}{2}$m2-$\frac{5}{2}$m+2),则E点的坐标为(m,-$\frac{1}{2}$m+2),设DE的长度为d,构建二次函数即可解决问题.
解答 解:(1)∵抛物线y=$\frac{1}{2}$x2-$\frac{5}{2}$x+2与x轴相交于A、B两点,与y轴相交于点C,
∴令y=0,可得x=1或4,
∴A( 1,0),B( 4,0);
令x=0,则y=2,
∴C点坐标为(0,2),
设直线BC的解析式为:y=kx+b,则有,
$\left\{\begin{array}{l}{b=2}\\{4k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线BC的解析式为:y=-$\frac{1}{2}$x+2;
(2)设点D的横坐标为m,则坐标为(m,$\frac{1}{2}$m2-$\frac{5}{2}$m+2),
∴E点的坐标为(m,-$\frac{1}{2}$m+2),
设DE的长度为d,
∵点D是直线BC下方抛物线上一点,
则d=-$\frac{1}{2}$m+2-($\frac{1}{2}$m2-$\frac{5}{2}$m+2),
整理得,d=-$\frac{1}{2}$m2+2m=-$\frac{1}{2}$(m-2)2+2,
∵a=-1<0,
∴当m=2时,d最大=2
∴D点的坐标为( 2,-1).
点评 此题主要考查了二次函数的性质及其图象与坐标轴的交点,设出D的坐标,利用二次函数最值得D点坐标是解答此题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
 某校在一块一边筑墙(墙长15m)的空地上修建一矩形花园,如图,花园一边靠墙,另三边用总长为50m的栅栏围成,设BC边长为xm,花园面积为ym2.
某校在一块一边筑墙(墙长15m)的空地上修建一矩形花园,如图,花园一边靠墙,另三边用总长为50m的栅栏围成,设BC边长为xm,花园面积为ym2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
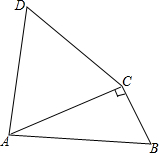 如图,△ABC中,∠ACB=90°,以AC为边作等边△ADC.
如图,△ABC中,∠ACB=90°,以AC为边作等边△ADC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于A、B两点,以AB为腰长在第二象限内作等腰直角△ABC(其中∠CAB=90°).
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于A、B两点,以AB为腰长在第二象限内作等腰直角△ABC(其中∠CAB=90°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com