
分析 (1)设该企业二、三月份产值平均增长率为x,根据二月份产值=一月份产值×(1+x),代入数值即可;
(2)根据三月份的产值=二月份的产值+22万元,列出方程求解即可.
解答 解:(1)该企业二月份的产值为200(1+x)万.
故答案为200(1+x)万;
(2)设该企业二、三月份产值平均增长率为x,由题意得:
200(1+x)2=200(1+x)+22,
解得:x=0.1,x=-1.1(不合题意舍去).
答:该企业二、三月份产值平均增长率是10%.
点评 本题考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b(当增长时中间的“±”号选“+”,当降低时中间的“±”号选“-”),可根据以上知识来列方程求解.


科目:初中数学 来源: 题型:选择题
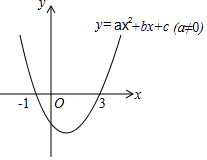 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 795×104 | B. | 7.95×105 | C. | 0.795×107 | D. | 7.95×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
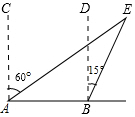 如图,一艘船上午9时在A处望见灯塔E在北偏东60°方向上,此船沿正东方向以每小时30海里的速度航行,11时到达B处,在B处测得灯塔E在北偏东15°方向上.
如图,一艘船上午9时在A处望见灯塔E在北偏东60°方向上,此船沿正东方向以每小时30海里的速度航行,11时到达B处,在B处测得灯塔E在北偏东15°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向上一面点数是奇数 | B. | 向上一面点数是偶数 | ||
| C. | 向上一面点数是大于6 | D. | 向上一面点数是小于7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
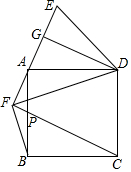 如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.
如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
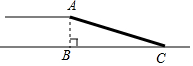 长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.
长清区政府准备在大学城修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为$\frac{1}{3}$,则坡面AC的长度为( )m.| A. | 16 | B. | 10 | C. | 18 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
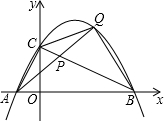 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A,B,与y轴交于点C.点P是线段BC上的动点(点P不与B,C重合),连接并延长AP交抛物线于另一点Q,设点Q的横坐标为x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com