练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知△ABC的三边a、b、c满足 =0，求最长边上的高h．

    【答案】解：由题意，得： ，2b﹣12=0，10﹣c=0，

    ∴a=8，b=6，c=10，

    ∵a2+b2=64+36=100=c2，

    ∴△ABC为Rt△ABC，且∠C=90°，

    ∵ ch= ab，

    ∴h=4.8


    【解析】根据绝对值，偶次方及算术平方根的非负性知几个非负数的和为零，则这几个数都为零，从而得出a,b,c的值，然后根据勾股定理的逆定理判断出△ABC为Rt△ABC，且∠C=90°，根据直角三角形面积的计算方法得出答案。
    【考点精析】通过灵活运用勾股定理的逆定理，掌握如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列四组数据不能作为直角三角形的三边长的是（ ）

    A. 6、8、10 B. 5、12、13 C. 7、10、12 D. 3、4、5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班在一次班会课上，就“遇见路人摔倒后如何处理”的主题进行讨论，并对全班50名学生的处理方式进行统计，得出相关统计表和统计图:

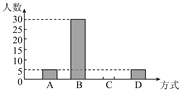
    请根据图表所提供的信息回答下列问题：

    (1)统计表中的m＝_____，n＝_____；

    (2)补全频数分布直方图；

    (3)若该校有2000名学生，请据此估计该校学生采取“马上救助”方式的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于的一元二次方程的实数解是和．

    (1)求的取值范围；

    (2)如果且为整数，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣ x2+mx+n的图象经过点A（2，3），对称轴为直线x=1，一次函数y=kx+b的图象经过点A，交x轴于点P，交抛物线于另一点B，点A、B位于点P的同侧．

    （1）求抛物线的解析式；

    （2）若PA：PB=3：1，求一次函数的解析式；

    （3）在（2）的条件下，当k＞0时，抛物线的对称轴上是否存在点C，使得⊙C同时与x轴和直线AP都相切，如果存在，请求出点C的坐标，如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A. 正实数和负实数统称实数B. 正数和负数统称为有理数

    C. 带根号的数和分数统称实数D. 有理数和无理数统称为实数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的袋中装有20个球，其中7个黄球，8个黑球，5个红球，这些球只有颜色不同，其它都相同．
    （1）求从袋中摸出一个球是黄球的概率；
    （2）现从袋中取出若干个黑球，搅匀后，使从袋中摸出一个球是黑球的概率是 ，求从袋中取出黑球的个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市2011年5月1日﹣10日十天的空气污染指数的数据如下（主要污染物为可吸入颗粒物）：61，75，70，56，81，91，92，91，75，81．那么该组数据的极差和中位数分别是（ ）

    A. 36，78 B. 36，86 C. 20，78 D. 20，77.3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=x与双曲线y=（x＞0）交于点A，将直线y=x向下平移个6单位后，与双曲线y=（x＞0）交于点B，与x轴交于点C，则C点的坐标为_____；若=2，则k=_____．

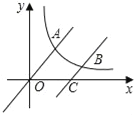
    查看答案和解析>>

    同步练习册答案