
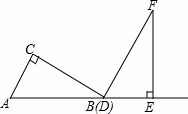
�������ǰ�ABC ��DEF������ͼ��ʾ��λ�ðڷţ���B���D�غϣ���AB���DE��ͬһ��ֱ���ϣ�����ͼ�������еĵ㣬�߶���ͬһƽ���ڣ������У���C=��DEF=90�㣬��ABC=��F=30�㣬AC=DE=6cm���̶ֹ����ǰ�DEF�������ǰ�ABC������DE����ƽ�ƣ�����C���ڱ�EF��ʱֹͣ�˶��������ǰ�ƽ�Ƶľ���Ϊx��cm�����������ǰ��ص����ֵ����Ϊy��cm2����
��DEF������ͼ��ʾ��λ�ðڷţ���B���D�غϣ���AB���DE��ͬһ��ֱ���ϣ�����ͼ�������еĵ㣬�߶���ͬһƽ���ڣ������У���C=��DEF=90�㣬��ABC=��F=30�㣬AC=DE=6cm���̶ֹ����ǰ�DEF�������ǰ�ABC������DE����ƽ�ƣ�����C���ڱ�EF��ʱֹͣ�˶��������ǰ�ƽ�Ƶľ���Ϊx��cm�����������ǰ��ص����ֵ����Ϊy��cm2����
��1������C���ڱ�EF��ʱ��x=�� cm��
��2����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��3�����BC���е�Ϊ��M����DF���е�Ϊ��N��ֱ��д�������ǰ�ƽ�ƹ����У���M���N֮��������Сֵ��
�⣺��1����ͼ1��ʾ����CG��AB��G�㣮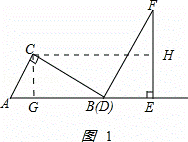 ��
��
��Rt��ABC����AC=6����ABC=30����
BC=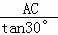 =6
=6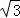 ��
��
��Rt��BCG�У�BG=BC•cos30��=9��
�ı���CGEH�Ǿ��Σ�
CH=GE=BG+BE=9+6=15cm��
�ʴ�Ϊ��15��
��2���ٵ�0��x��6ʱ����ͼ2��ʾ�� ��
��
��GDB=60�㣬��GBD=30�㣬DB=x����
DG=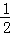 x��BG=
x��BG=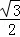 x���ص����ֵ����Ϊy=
x���ص����ֵ����Ϊy=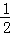 DG•BG=
DG•BG=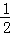 ��
��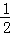 x��
x��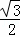 x=
x=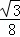 x2
x2
�ڵ�6��x��12ʱ����ͼ3��ʾ��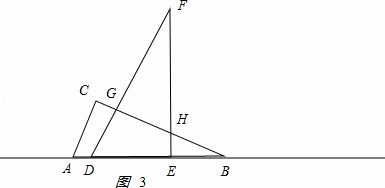 ��
��
BD=x��DG=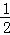 x��BG=
x��BG=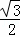 x��BE=x﹣6��EH=
x��BE=x﹣6��EH=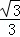 ��x﹣6����
��x﹣6����
�ص����ֵ����Ϊy=S��BDG﹣S��BEH=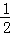 DG•BG﹣
DG•BG﹣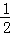 BE•EH��
BE•EH��
��y=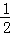 ��
��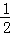 x��
x��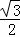 x﹣
x﹣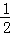 ��x﹣6��
��x﹣6��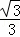 ��x﹣6��
��x﹣6��
����y=﹣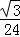 x2+2
x2+2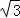 x﹣6
x﹣6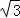 ��
��
�۵�12��x��15ʱ����ͼ4��ʾ��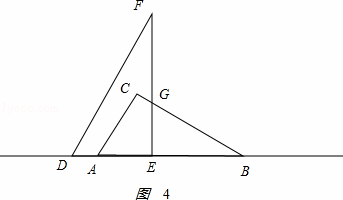 ��
��
AC=6��BC=6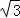 ��BD=x��BE=��x﹣6����EG=
��BD=x��BE=��x﹣6����EG=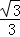 ��x﹣6����
��x﹣6����
�ص����ֵ����Ϊy=S��ABC﹣S��BEG=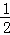 AC•BC﹣
AC•BC﹣ BE•EG��
BE•EG��
��y= ��6��6
��6��6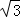 ﹣
﹣ ��x﹣6��
��x﹣6��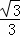 ��x﹣6����
��x﹣6����
����y=18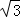 ﹣
﹣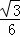 ��x2﹣12x+36��=﹣
��x2﹣12x+36��=﹣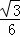 x2+2
x2+2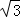 x+12
x+12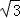 ��
��
����������y=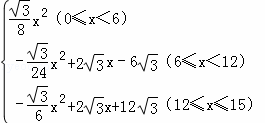 ��
��
��3����ͼ5��ʾ��NG��DE��G�㣮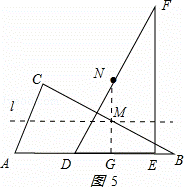 ��
��
��M��NG��ʱMN��̣�
NG�ǡ�DEF����λ�ߣ�
NG=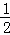 EF=
EF=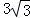 ��
��
MB=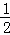 CB=3
CB=3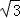 ����B=30�㣬
����B=30�㣬
MG=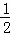 MB=
MB=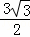 ��
��
MN��С=3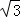 ﹣
﹣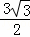 =
=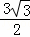 ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�˱��ε��ڽǺ͵��ڣ�������
�� A�� 360�� B�� 1080�� C�� 1440�� D�� 2160��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
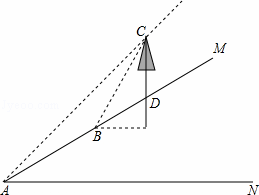
����ʦ������Ϣʱ����֯ѧ������ɽ����һ�ô���CD�ĸ߶ȣ���ͼ��ɽ����ˮƽ���30��ǣ�����MAN=30�㣩����ɽ�µײ�A����ô������˵�C������Ϊ45�㣬������ǰ��20�ף�����B�����ֲ�������˵�C������Ϊ60�㣨ͼ�и������ͬһƽ���ڣ�������ô���CD�ĸ߶ȣ������ȷ��0.1�ף��ο����ݣ�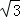 ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
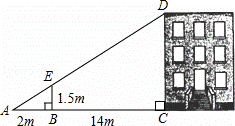
��ͼ�����ñ��BE����������ĸ߶ȣ����BE��1.5m�����AB=2m��BC=14cm����¥��CDΪ����m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
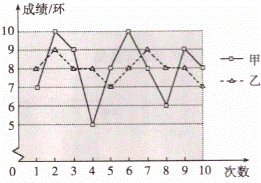
Ҫ�Ӽס�������ͬѧ��ѡ��һ���������༶�μ������������ͼ���������10�����ѵ���ɼ�������ͳ��ͼ��
��1������ü�ƽ���ɼ�Ϊ8�������ҵ�ƽ���ɼ���
��2���۲�ͼ�Σ�ֱ��д���ף�����10������ɼ��ķ���s��2��
s��2�ĸ���
��3����������༶����ѡ�ֵ�����ɼ�����7�����ң�����Ӧ��ѡ�� �����������ʣ���������༶����ѡ�ֵ�����ɼ�����9�����ң�����Ӧ��ѡ�� �����������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ��õ������ĸ����ۣ���OA=OD����AD��EF��
��ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ��õ������ĸ����ۣ���OA=OD����AD��EF��
�۵���A=90��ʱ���ı���AEDF�������Σ�
�� ��������������ȷ����
��������������ȷ����
A���ڢ� B���ڢ� C���٢ڢ� D���ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������y=3x2+2x﹣1����ƽ��4����λ���Ⱥ�ĺ�������ʽΪ��������
�� A�� y=3x2+2x﹣5 B�� y=3x2+2x﹣4 C�� y=3x2+2x+3 D�� y=3x2+2x+4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭��ʡ���꼶��ѧ�ڵ�һ��ѧ�������ѧ�Ծ��������棩 ���ͣ������
�ֽ���ʽ2x2��4xy+2y2 = ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com