
 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;
③当∠A=90°时,四边形AEDF是正方形;
④ .上述结论中正确的是
.上述结论中正确的是
A.②③ B.②④ C.①②③ D.②③④
科目:初中数学 来源: 题型:
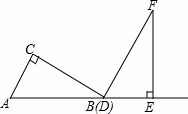
两个三角板ABC ,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
(1)当点C落在边EF上时,x= cm;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N.直接写出在三角板平移过程中,点M与点N之间距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
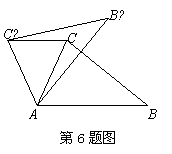
如图,在△ABC中,∠CAB=65°.将△ABC在平面内绕点A旋转到△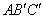 的位置
的位置 ,使得
,使得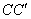 ∥AB,则旋转角的度数为
∥AB,则旋转角的度数为
A.35°
B. 40°
40°
C.50°
 D.65°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50º,观测旗杆底部B的仰角为45º,则旗杆的高度约为________m.(结果精确到0.1m.参考数据:sin50º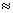 0.77,cos50º
0.77,cos50º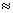 0.64,tan50º
0.64,tan50º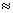 1.19)
1.19)

查看答案和解析>>
科目:初中数学 来源: 题型:
(1)问题
如图1,在四边形ABCD中,点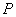 为
为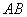 上一点,
上一点, 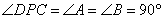 .
.
求证:AD·BC=AP·BP.
(2)探究
如图2,在四边形ABCD中,点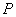 为
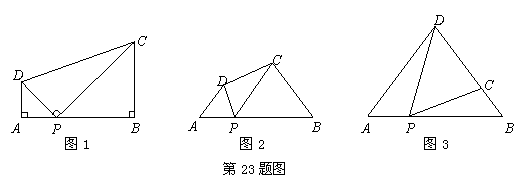
为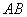 上一点,当
上一点,当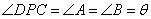 时,上述结论是否依然成立?说明理由.
时,上述结论是否依然成立?说明理由.
(3)应用
请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5, 点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A.设点P的运动时间为t(秒),当以 D为圆心,
D为圆心,
 DC为半径的圆与AB相切时,求t的值.
DC为半径的圆与AB相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都区七校联谊九年级3月月考数学试卷(解析版) 题型:解答题
(14’)如图,在平面直角坐标系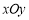 中,A、B为
中,A、B为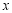 轴上两点,C、D为
轴上两点,C、D为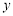 轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,
轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,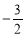 ),点M是抛物线C2:
),点M是抛物线C2: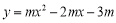 (
(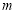 <0)的顶点.
<0)的顶点.
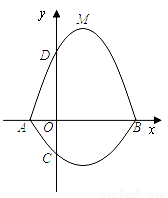
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求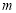 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com