
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),该抛物线的对称轴为直线x=﹣1,若点C(﹣ ![]() ,y1),D(﹣
,y1),D(﹣ ![]() ,y2),E(
,y2),E( ![]() ,y3)均为函数图象上的点,则y1 , y2 , y3的大小关系为 .
,y3)均为函数图象上的点,则y1 , y2 , y3的大小关系为 . 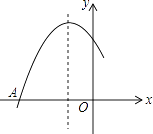
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标. 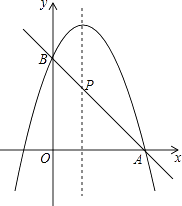
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】飞机着陆后滑行的距离S(单位:m)关于滑行时间t(单位:s)的函数解析式是:S=60t﹣1.5t2
(1)直接指出飞机着陆时的速度;
(2)直接指出t的取值范围;
(3)画出函数S的图象并指出飞机着陆后滑行多远才能停下来? 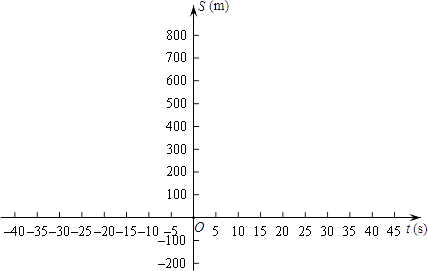
查看答案和解析>>
科目:初中数学 来源: 题型:
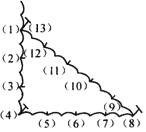
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
A. 直角三角形两个锐角互补
B. 三角形内角和等于180°
C. 如果三角形两条边长的平方和等于第三边长的平方
D. 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
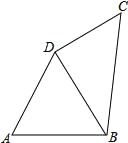
【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
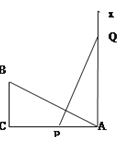
【题目】如图,∠C=90°,AC=8,BC=3,线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=_________时,才能使ΔABC与ΔAPQ 全等。
查看答案和解析>>
科目:初中数学 来源: 题型:
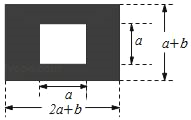
【题目】如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=3,b=2,请求出绿化面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com