
如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.
(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);
(2)求海轮在B处时与灯塔C的距离(结果保留整数).
(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)

(1)34.4海里;(2)60海里.
【解析】
试题分析:(1)过点C作CD⊥AB于点D,则CD的长为海轮在航行过程中与灯塔C的最短距离.
(2)在Rt△BCD中,根据55°角的余弦值即可求出海轮在B处时与灯塔C的距离.
试题解析:【解析】
(1)如答图,过点C作CD⊥AB于点D,
依题意得:∠ACD=∠CAE=42°,∠BCD=∠CBF=55°,
设CD的长为x海里,
在Rt△ACD中,tan42°= ,则AD=x•tan42°,
,则AD=x•tan42°,
在Rt△BCD中,tan55°= ,则BD=x•tan55°,
,则BD=x•tan55°,
∵AB=80,∴AD+BD=80. ∴x•tan42°+x•tan55°=80,解得:x≈34.4.
答:海轮在航行过程中与灯塔C的最短距离是34.4海里.
(2)在Rt△BCD中,cos55°= ,∴BC=
,∴BC= ≈60海里.
≈60海里.
答:海轮在B处时与灯塔C的距离是60海里.

考点:1.解直角三角形的应用(方向角问题);2.锐角三角函数定义.


科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:解答题
【问题提出】
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.

【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 ,则△ABC≌△DEF.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:填空题
2014年南京青奥会某项目6名礼仪小姐身高如下(单位:cm):168,166,168,167,169,168,则他们身高的众数是 cm,极差是 cm.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏南京卷)数学(解析版) 题型:选择题
若 ,相似比为1:2,则
,相似比为1:2,则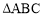 与
与 的面积的比为( )
的面积的比为( )
A.1:2 B.2:1 C.1:4 D.4:1
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:解答题
如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2.
(1)求证:△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com