
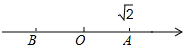
 如图,数轴上点A表示$\sqrt{2}$,点A关于原点的对称点为B,设点B所表示的数字为x,求(x-$\sqrt{2}$)2+$\sqrt{2}$x的值.
如图,数轴上点A表示$\sqrt{2}$,点A关于原点的对称点为B,设点B所表示的数字为x,求(x-$\sqrt{2}$)2+$\sqrt{2}$x的值.  品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a3•a3=a6 | B. | (-y2)5=y10 | ||
| C. | (-a3y2)3=-a9y6 | D. | ($\frac{1}{3}$x-$\frac{3}{4}$xy)•(-12y)=-4xy+9xy2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
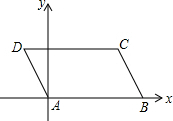 在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).
在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,如图建立直角坐标系,则C的坐标是(4,$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
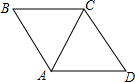 如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )
如图,△ABC与△ACD都是等边三角形,△ACD是由△ABC( )| A. | 绕点A顺时针旋转60°得到的 | B. | 绕点A顺时针旋转120°得到的 | ||
| C. | 绕点C顺时针旋转60°得到的 | D. | 绕点C顺时针旋转120°得到的 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
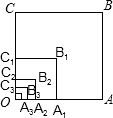 如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的$\frac{1}{2}$,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的$\frac{1}{2}$,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的$\frac{1}{2}$,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=16.
如图,以O为位似中心,将边长为256的正方形OABC依次作位似变换,经第一次变化后得正方形OA1B1C1,其边长OA1缩小为OA的$\frac{1}{2}$,经第二次变化后得正方形OA2B2C2,其边长OA2缩小为OA1的$\frac{1}{2}$,经第三次变化后得正方形OA3B3C3,其边长OA3缩小为OA2的$\frac{1}{2}$,…,依次规律,经第n次变化后,所得正方形OAnBnCn的边长为正方形OABC边长的倒数,则n=16.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{30x-10}{x+5}$=26 | B. | $\frac{30x+10}{x+5}$=26 | C. | $\frac{30x}{x+5}$=26+10 | D. | $\frac{30x+10}{x-5}$=26 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-9)×(-25)}$=$\sqrt{-9}×\sqrt{-25}$=(-3)×(-5)=15 | B. | -3$\sqrt{\frac{2}{3}}$=$\sqrt{(-3)^{2}×\frac{2}{3}}$=$\sqrt{6}$ | ||
| C. | $\sqrt{1{3}^{2}-1{2}^{2}}$=$\sqrt{(13+12)(13-12)}$=$\sqrt{25}$=5 | D. | 3$\sqrt{2}•4\sqrt{2}=12\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com