
| A. | $\sqrt{(-9)×(-25)}$=$\sqrt{-9}×\sqrt{-25}$=(-3)×(-5)=15 | B. | -3$\sqrt{\frac{2}{3}}$=$\sqrt{(-3)^{2}×\frac{2}{3}}$=$\sqrt{6}$ | ||
| C. | $\sqrt{1{3}^{2}-1{2}^{2}}$=$\sqrt{(13+12)(13-12)}$=$\sqrt{25}$=5 | D. | 3$\sqrt{2}•4\sqrt{2}=12\sqrt{2}$ |
分析 利用二次根式的乘法运算法则,结合二次根式的性质分别化简求出即可.
解答 解:A、$\sqrt{(-9)×(-25)}$=$\sqrt{9}$×$\sqrt{25}$=15,故此选项错误;
B、-3$\sqrt{\frac{2}{3}}$=-$\sqrt{{3}^{2}×\frac{2}{3}}$=-$\sqrt{6}$,故此选项错误;
C、$\sqrt{1{3}^{2}-1{2}^{2}}$=$\sqrt{(13+12)×(13-12)}$=$\sqrt{25}$=5,正确;
D、3$\sqrt{2}$×4$\sqrt{2}$=24,故此选项错误.
故选:C.
点评 此题主要考查了二次根式的乘法运算,正确掌握运算法则是解题关键.


科目:初中数学 来源: 题型:解答题
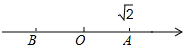 如图,数轴上点A表示$\sqrt{2}$,点A关于原点的对称点为B,设点B所表示的数字为x,求(x-$\sqrt{2}$)2+$\sqrt{2}$x的值.
如图,数轴上点A表示$\sqrt{2}$,点A关于原点的对称点为B,设点B所表示的数字为x,求(x-$\sqrt{2}$)2+$\sqrt{2}$x的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
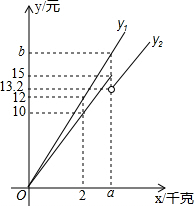 王阿姨“五一”期间去超市买大米和土豆,恰逢超市土豆销售做促销活动:购买3千克以上时,每千克便宜0.6元,如图,y1表示大米的售价(元)与重量x(千克)之间的函数关系,y2表示土豆的售价(元)与重量x(千克)之间的函数关系.根据图象,回答下列问题:
王阿姨“五一”期间去超市买大米和土豆,恰逢超市土豆销售做促销活动:购买3千克以上时,每千克便宜0.6元,如图,y1表示大米的售价(元)与重量x(千克)之间的函数关系,y2表示土豆的售价(元)与重量x(千克)之间的函数关系.根据图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
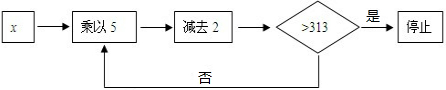
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
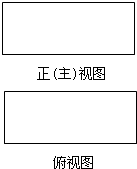 如图是长和宽分别相等的两个矩形.给定下列四个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图;④存在正方体,其正(主)视图、俯视图如图.其中真命题的个数是( )
如图是长和宽分别相等的两个矩形.给定下列四个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图;④存在正方体,其正(主)视图、俯视图如图.其中真命题的个数是( )| A. | 3 | B. | 2 | C. | 1 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com