
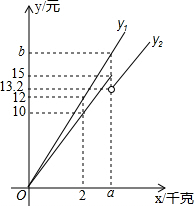
 �����̡���һ���ڼ�ȥ���������������ǡ�곬�����������������������3ǧ������ʱ��ÿǧ�˱���0.6Ԫ����ͼ��y1��ʾ�����ۼۣ�Ԫ��������x��ǧ�ˣ�֮��ĺ�����ϵ��y2��ʾ�������ۼۣ�Ԫ��������x��ǧ�ˣ�֮��ĺ�����ϵ������ͼ�ش��������⣺
�����̡���һ���ڼ�ȥ���������������ǡ�곬�����������������������3ǧ������ʱ��ÿǧ�˱���0.6Ԫ����ͼ��y1��ʾ�����ۼۣ�Ԫ��������x��ǧ�ˣ�֮��ĺ�����ϵ��y2��ʾ�������ۼۣ�Ԫ��������x��ǧ�ˣ�֮��ĺ�����ϵ������ͼ�ش��������⣺���� ��1����������ó�a=3���ٵó�y1�Ľ���ʽ��a=3����ɵ�b��ֵ��
��2��������ֱ��ƽ�еó��������ۼ�y2��Ԫ��������x��ǧ�ˣ�֮��ĺ�����ϵʽ���ɣ�
��3������������Ĵ���Ϊxǧ�ˣ��г����̽�ɣ�
��� �⣺��1��������ɵã�a=3��
��y1����ʽΪ��y1=kx���ѣ�2��12���������ʽ���ɵã�k=6��
����y1����ʽΪ��y1=6x��
��x=3�������ʽy1=6x=18��
�ʴ�Ϊ��3��18��
��2������ͼ��ɵõ�x=3ǧ��ʱ�������ļ۸�Ϊ15Ԫ�����Կɵ�ÿǧ�������ļ۸�Ϊ5Ԫ��
��Ϊ����3ǧ������ʱ��ÿǧ�˱���0.6Ԫ��
�ɵã�����3ǧ������ʱ���������ۼ�y2��Ԫ��������x��ǧ�ˣ�֮��ĺ�����ϵʽΪy2=5x+b��
�ѣ�3��13.2������y2=5x+b��
�ɵã�y2=5x-0.6��
��3����6-x��3ʱ������������Ĵ���Ϊxǧ�ˣ�����Ϊ6-xǧ�ˣ��ɵã�
6x+5��6-x��=28��
��ã�x=-2������������ȥ��
��6-x��3ʱ������������Ĵ���Ϊxǧ�ˣ�����Ϊ6-xǧ�ˣ��ɵã�
6x+4.4��6-x��=28��
��ã�x=1��
����������Ĵ�������Ϊ1ǧ�ˣ�5ǧ�ˣ�
���� ���⿼��һ�κ�����Ӧ�ã��ؼ��Ǹ�����������ֶκ����ĸ�����������ô���ϵ���������ʽ�Ǹ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
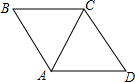 ��ͼ����ABC���ACD���ǵȱ������Σ���ACD���ɡ�ABC��������
��ͼ����ABC���ACD���ǵȱ������Σ���ACD���ɡ�ABC��������| A�� | �Ƶ�A˳ʱ����ת60��õ��� | B�� | �Ƶ�A˳ʱ����ת120��õ��� | ||
| C�� | �Ƶ�C˳ʱ����ת60��õ��� | D�� | �Ƶ�C˳ʱ����ת120��õ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{��-9������-25��}$=$\sqrt{-9}��\sqrt{-25}$=��-3������-5��=15 | B�� | -3$\sqrt{\frac{2}{3}}$=$\sqrt{��-3��^{2}��\frac{2}{3}}$=$\sqrt{6}$ | ||
| C�� | $\sqrt{1{3}^{2}-1{2}^{2}}$=$\sqrt{��13+12����13-12��}$=$\sqrt{25}$=5 | D�� | 3$\sqrt{2}•4\sqrt{2}=12\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 9 | C�� | 15 | D�� | 16 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com