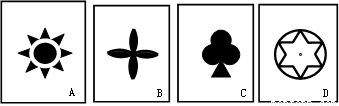
如图，有四张背面相同的纸牌A、B、C、D，其正面分别画有四个不同的图形，小明将这四张牌背面朝上洗匀后随机摸出一张，放回后洗匀再随机摸出一张。
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用A、B、C、D表示）
（2）求两次摸牌的牌面图形既是中心对称图形又是轴对称图形的概率。
（1）结果见解析；（2）
．
【解析】
试题分析：（1）用列表法或画出树状图分析数据、列出可能的情况即可．
（2）A、B、D既是轴对称图形，也是中心对称图形，C是轴对称图形，不是中心对称图形．列举出所有情况，让两次摸牌的牌面图形既是中心对称图形又是轴对称图形的情况数除以总情况数即为所求的概率．
试题解析：（1）列表如下：
A | B | C | D | |
A | （A，A） | （A，B） | （A，C） | （A，D） |
B | （B，A） | （B，B） | （B，C） | （B，D） |
C | （C，A） | （C，B） | （C，C） | （C，D） |
D | （D，A） | （D，B） | （D，C） | （D，D） |
（2）从表中可以得到，两次摸牌所有可能出现的结果共有16种，其中既是中心对称图形又是轴对称图形的有9种．
故所求概率是．
考点：1．列表法与树状图法；2．轴对称图形；3．中心对称图形．
名校课堂系列答案科目：初中数学 来源：2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷（解析版） 题型：解答题
如图，边长为4cm的等边三角形ABC与⊙O等高（即高与直径相等），⊙O与BC相切于点C，⊙O与AC相交于点E．
求：（1）CE的长；
（2）阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖北省广水市九年级下学期第一次月考数学试卷（解析版） 题型：解答题
（12分）长岭中心中学九年级数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：
时间x（天） | 1≤x＜50 | 50≤x≤90 |
售价（元/件） | x+40 | 90 |
每天销量（件） | 200﹣2x | |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年湖北省广水市九年级下学期第一次月考数学试卷（解析版） 题型：选择题
如图，圆锥体的高h=2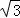
cm，底面半径r=2cm，则圆锥体的全面积为（ ）cm2．
A．4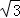
π B．8π C．12π D．（4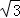+4）π
查看答案和解析>>
科目：初中数学 来源：2014-2015学年河南省商丘市九年级上学期期末考试数学试卷（解析版） 题型：计算题
在平面直角坐标系xOy中（O为坐标原点），已知抛物线y=x2＋bx＋c过点A（4，0），B（1，－3）．
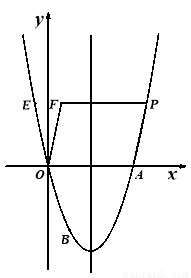
（1）求出该抛物线的函数解析式；
（2）设该抛物线的对称轴为直线l，点P（m，n）是抛物线上在第一象限的点，点E与点P关于直线l对称，点E与点F关于y轴对称．若四边形OAPF的面积为48，求点P的坐标；
（3）在（2）的条件下，设M是直线l上任意一点，试判断MP＋MA是否存在最小值，若存在，求出这个最小值及相应的点M的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年河南省商丘市九年级上学期期末考试数学试卷（解析版） 题型：填空题
如图，一段抛物线
记为m1，它与x轴交点为O，A1，顶点为P1；将m1绕点A1旋转180°得m2，交x轴于点A2，顶点为P2；将m2绕点A2旋转180°得m3，交x轴于点A3，顶点为P3；…，如此进行下去，直至得m10，顶点为P10，则P10的坐标为（ ）
查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏省太仓市、昆山市七年级上学期期末联考数学试卷（解析版） 题型：选择题
已知太阳的半径约为696000000m，则696000000这个数用科学记数法可表示为 （ ）.
A．0．696×109 B．6．96×109
C．6．96×108 D．69．6×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图象如图所示，则二次函数
的图象大致为（ ）
