
在平面直角坐标系xOy中(O为坐标原点),已知抛物线y=x2+bx+c过点A(4,0),B(1,-3).
(1)求出该抛物线的函数解析式;
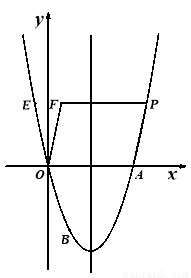
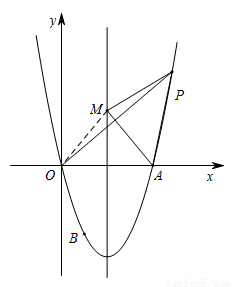
(2)设该抛物线的对称轴为直线l,点P(m,n)是抛物线上在第一象限的点,点E与点P关于直线l对称,点E与点F关于y轴对称.若四边形OAPF的面积为48,求点P的坐标;
(3)在(2)的条件下,设M是直线l上任意一点,试判断MP+MA是否存在最小值,若存在,求出这个最小值及相应的点M的坐标;若不存在,请说明理由.
(1)y=x2-4x;(2)(6,12)(3)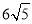 .
.
【解析】
试题分析:(1)用待定系数法就可求出b和c,再将抛物线的解析式配成顶点式,就可解决问题.
(2)由条件可得E(4-m,n)、F(m-4,n),从而得到PF=4,由四边形OAPF的面积为48可求出点P的纵坐标,然后代入抛物线的解析式就可求出点P的坐标.
(3)由点E与点P关于直线l对称可得MP=ME,则有MP+MA=ME+MA,根据“两点之间线段最短”可得AE的长就是MP+MA的最小值,只需运用勾股定理就可解决问题.
试题解析:(1)把点A、B坐标代入抛物线解析式,得: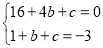 .
.
解得: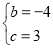
所以,抛物线的解析式为y=x2-4x
(2)如图,由题意知:E点坐标为(4-m,n),F点坐标为(m-4,n)
∴PF=4
∵OA∥PF,OA=4
∴四边形OAPF是平行四边形
∵点P(m,n)是抛物线上在第一象限的点
∴n=m2-4m
∴4(m2-4m)=48
解得:m1=-2(舍去),m2=6,
∴点P的坐标为(6,12)
(3)MP+MA存在最小值.
由(1)得,抛物线与x轴交于点A(4,0),O(0,0)
∵M是直线l上任意一点
∴MO=MA
∴当点O、M、P三点共线时,MP+MA=MP+MO=OP为最小值
∵点P的坐标为(6,12)
∴直线OP的解析式为y=2x
设M(2,t)
∴t=2×2=4
∴M(2,4)
此时线段OP的长度为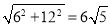 .
.
考点:二次函数综合题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年江西省南昌市九年级上学期期末终结性测试数学试卷(解析版) 题型:解答题
如图,已知:点B(3,3)在双曲线y= (x>0)上,点D在双曲线y=-
(x>0)上,点D在双曲线y=-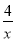 (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.求:
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.求:
(1)k的值;
(2)点A的坐标.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省宜昌市兴山县九年级上学期期末调研考试数学试卷(解析版) 题型:选择题
小新抛一枚质地均匀的硬币,连续抛三次,硬币落地均正面朝上,如果他第四次抛硬币,那么硬币正面朝上的概率为( )
A.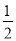 B.
B.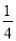 C.1 D.
C.1 D.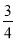
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省广水市九年级下学期第一次月考数学试卷(解析版) 题型:选择题
函数y= 中,自变量x的取值范围是( ).
中,自变量x的取值范围是( ).
A.x≠0 B.x≥2 C.x>2且x≠0 D.x≥2且x≠0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省商丘市九年级上学期期末考试数学试卷(解析版) 题型:解答题
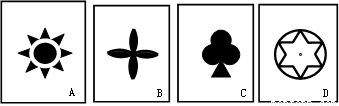
如图,有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的图形,小明将这四张牌背面朝上洗匀后随机摸出一张,放回后洗匀再随机摸出一张。
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用A、B、C、D表示)
(2)求两次摸牌的牌面图形既是中心对称图形又是轴对称图形的概率。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省梅州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分8分)某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省太仓市、昆山市七年级上学期期末联考数学试卷(解析版) 题型:选择题
如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,其中能判定AB∥CD的条件的个数有( ).

A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com