
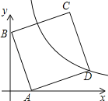
【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴,y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线y=![]() (k≠0)上.将正方形沿y轴向下方平移m个单位长度后,点C恰好落在该双曲线上,则m的值为__.
(k≠0)上.将正方形沿y轴向下方平移m个单位长度后,点C恰好落在该双曲线上,则m的值为__.
【答案】![]()
【解析】
作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F,易证△OAB≌△FDA≌△BEC,求得A、B的坐标,根据全等三角形的性质可以求得C、D的坐标,从而利用待定系数法求得反比例函数的解析式,进而求得N的坐标,则a的值即可求解.
解:作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F.
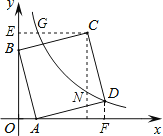
在y=-4x+4中,令x=0,解得:y=4,即B的坐标是(0,4).
令y=0,解得:x=1,即A的坐标是(1,0).
则OB=4,OA=1.
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
又∵直角△ABO中,∠BAO+∠OBA=90°,
∴∠DAF=∠OBA,
在△OAB和△FDA中,
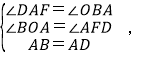
同理,△OAB≌△FDA≌△BEC,
∴AF=OB=EC=4,DF=OA=BE=1,
故D的坐标是(5,1),C的坐标是(4,5).代入y=![]()
得:k=5,则函数的解析式是:y=![]() .
.
则C的横坐标是4,把x=4代入y=![]() 得:y=
得:y=![]() ,则N点坐标为:(4,
,则N点坐标为:(4,![]() ),故CN=5-
),故CN=5-![]() =
=![]() ,
,
∴将正方形沿y轴向下方平移![]() 个单位长度后,点C恰好落在该双曲线上.
个单位长度后,点C恰好落在该双曲线上.
故答案为:![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的![]() 和点P,给出如下定义:如果在
和点P,给出如下定义:如果在![]() 上存在一个动点Q,使得
上存在一个动点Q,使得![]() 是以CQ为底的等腰三角形,且满足底角
是以CQ为底的等腰三角形,且满足底角![]() ,那么就称点P为
,那么就称点P为![]() 的“关联点”.
的“关联点”.
![]() 当
当![]() 的半径为2时,
的半径为2时,
![]() 在点
在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的“关联点”是______;
的“关联点”是______;
![]() 如果点P在射线
如果点P在射线![]() 上,且P是
上,且P是![]() 的“关联点”,求点P的横坐标m的取值范围.
的“关联点”,求点P的横坐标m的取值范围.
![]() 的圆心C在x轴上,半径为4,直线
的圆心C在x轴上,半径为4,直线![]() 与两坐标轴交于A和B,如果线段AB上的点都是
与两坐标轴交于A和B,如果线段AB上的点都是![]() 的“关联点”,直接写出圆心C的横坐标n的取值范围.
的“关联点”,直接写出圆心C的横坐标n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
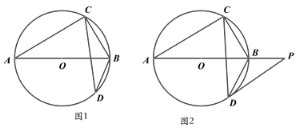
【题目】已知AB是⊙O的的直径,弦CD与AB相交,∠BCD=25°。
(1)如图1,求∠ABD的大小;
(2)如图2,过点D作O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
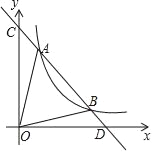
【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有2个黄球,1个红球和1个白球,除色外都相同.
(1)搅匀后,从袋中随机出一个球,恰好是黄球的概是_____?
(2)搅匀后,从中随机摸出两个球,求摸到一个红球和一个黄球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
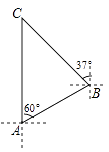
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
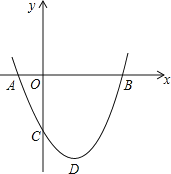
【题目】如图,二次函数![]() 图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为
图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为![]() ,
,![]() 与y轴负半轴交于点C.
与y轴负半轴交于点C.
![]() 若
若![]() 是等腰直角三角形,求a的值.
是等腰直角三角形,求a的值.
![]() 探究:是否存在a,使得
探究:是否存在a,使得![]() 是等腰三角形?若存在,求出符合条件的a的值;不存在,说明理由.
是等腰三角形?若存在,求出符合条件的a的值;不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
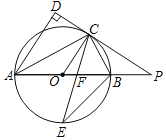
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(2k﹣1)x+k2﹣2k+2=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程的两个实数根分别为x1,x2.是否存在这样的实数k,使得|x1|﹣|x2|=![]() ?若存在,求出这样的k值;若不存在,说明理由.
?若存在,求出这样的k值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com