Question

16．已知：△ABC中，AB=AC，以AB为直径作⊙O交AC于D，交BC于E．

（1）如图1，求证：$\widehat{BE}$=$\widehat{DE}$；
（2）如图2，过点B作⊙O的切线，交AC的延长线于点F，若tan∠CBF=$\frac{1}{2}$，求cos∠F的值．

Answer 1

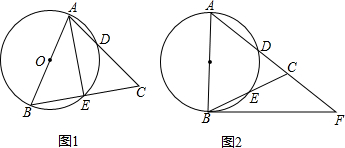
分析 （1）根据圆周角定理，由AB为直径得到∠AEB=90°，则AE⊥BC，根据等腰三角形的性质得∠BAE=∠CAE，然后根据圆周角定理即可得到$\widehat{BE}$=$\widehat{DE}$；
（2）连结AE、BD，如图，根据切线的性质得∠ABF=90°，则利用等角的余角相等得∠CBF=∠BAE，在Rt△ABE中，由正切定义得到tan∠BAE=tan∠CBF=$\frac{1}{2}$=$\frac{BE}{AE}$，于是可设BE=a，AE=2a，易得CE=BE=a，AB=AC=$\sqrt{5}$a，接着利用面积法计算出BD=$\frac{4\sqrt{5}}{5}$a，于是在Rt△ABD中，由余弦定理可计算出cos∠ABD=$\frac{4}{5}$，然后证明∠F=∠ABD，从而得到cos∠F的值．

解答 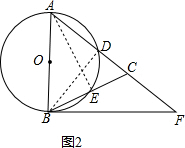（1）证明：∵AB为直径，
∴∠AEB=90°，
∴AE⊥BC，
∵AB=AC，
∴AE平分∠BAC，
∴∠BAE=∠CAE，
∴$\widehat{BE}$=$\widehat{DE}$；
（2）解：连结AE、BD，如图，
∵BF为切线，
∴AB⊥BF，
∴∠ABF=90°，
∴∠CBF=∠BAE，
在Rt△ABE中，∵tan∠BAE=tan∠CBF=$\frac{1}{2}$=$\frac{BE}{AE}$，
∴设BE=a，AE=2a，
∴CE=BE=a，AB=$\sqrt{B{E}^{2}+A{E}^{2}}$=$\sqrt{5}$a，
∴AC=$\sqrt{5}$a，
∵AB为直径，
∴∠ADB=90°，
∴∠F+∠DBF=90°，而∠DBF+∠ABD=90°，
∴∠F=∠ABD，
∵$\frac{1}{2}$BD•AC=$\frac{1}{2}$AE•BC，
∴BD=$\frac{2a•2a}{\sqrt{5}a}$=$\frac{4\sqrt{5}}{5}$a，
在Rt△ABD中，cos∠ABD=$\frac{BD}{AB}$=$\frac{\frac{4\sqrt{5}a}{5}}{\sqrt{5}a}$=$\frac{4}{5}$，
∴cos∠F=$\frac{4}{5}$．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．也考查了等腰三角形的性质和圆周角定理．