
【题目】 在△ABC中,∠A=40°.
(1)如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;
(2)如图(2)若BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;
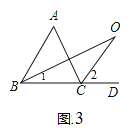
(3)如图(3)若BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;
(4)根据上述三问的结果,当∠A=n°时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).

【答案】(1)110°;(2)70°;(3)20°;(4)分别是90°+ ![]() °;90°-
°;90°- ![]() °;
°;![]() °
°
【解析】试题分析:(1)首先根据三角形的内角和定理,求得∠ABC+∠ACB,再根据角平分线的概念,求得∠OBC+∠OCB,最后根据三角形的内角和定理求得∠BOC= 110°;(2)如图2,根据角平分线的定义和三角形外角的性质得∠DBC=2∠1=∠ACB+∠A,∠ECB=2∠2=∠ABC+∠A,所以2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°,再由∠1+∠2+∠BOC=180°可得2∠BOC=180°-∠A,即∠BOC=90°-![]() ∠A=90°-20°=70°;(3)如图3,由BO和CO分别是∠ABC和∠ACD的角平分线,可得∠1=
∠A=90°-20°=70°;(3)如图3,由BO和CO分别是∠ABC和∠ACD的角平分线,可得∠1= ![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACD,根据三角形外角的性质可得∠ACD=∠A+∠ABC,即可得∠2=
∠ACD,根据三角形外角的性质可得∠ACD=∠A+∠ABC,即可得∠2= ![]() (∠A+∠ABC)=
(∠A+∠ABC)= ![]() ∠A+∠1,再由三角形外角的性质可得∠BOC=∠2﹣∠1=
∠A+∠1,再由三角形外角的性质可得∠BOC=∠2﹣∠1=![]() ∠A+∠1﹣∠1=
∠A+∠1﹣∠1= ![]() ∠A=
∠A=![]() ×40°=20°;(4)利用以上结论直接得出答案即可.
×40°=20°;(4)利用以上结论直接得出答案即可.
试题解析:
(1)∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°.
∵BO、CO分别是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=![]() ∠ABC+∠ACB)=
∠ABC+∠ACB)=![]() ×140°=70°,
×140°=70°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-70°=110°;
(2)∵BO、CO分别是△ABC的外角∠DBC、∠ECB的角平分线,
∴∠DBC=2∠1=∠ACB+∠A,
∠ECB=2∠2=∠ABC+∠A,
∴2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°,
又∵∠1+∠2+∠BOC=180°,
∴2∠BOC=180°-∠A,
∴∠BOC=90°-![]() ∠A=90°-20°=70°.
∠A=90°-20°=70°.
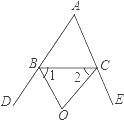
图2
(3)如图3,
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1= ![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACD,
∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2= ![]() (∠A+∠ABC)=
(∠A+∠ABC)= ![]() ∠A+∠1,
∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2﹣∠1=![]() ∠A+∠1﹣∠1=
∠A+∠1﹣∠1= ![]() ∠A=
∠A=![]() ×40°=20°.
×40°=20°.
(4)分别是90°+ ![]() °;90°-
°;90°- ![]() °;
°;![]() °
°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
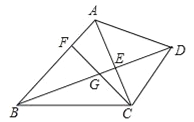
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD.
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+1与x轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.
(1)求这个抛物线的表达式;
(2)求点P的坐标;
(3)点Q在x轴上,若以Q、O、P为顶点的三角形与以点C、A、B为顶点的三角形相似,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从小华家到姥姥家,有一段上坡路和一段下坡路.星期天,小华骑自行车去姥姥家,如果保持上坡每小时行3km,下坡每小时行5km,他到姥姥家需要行66分钟,从姥姥家回来时需要行78分钟才能到家.那么,从小华家到姥姥家上坡路和下坡路各有多少千米,姥姥家离小华家有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为何?( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com