
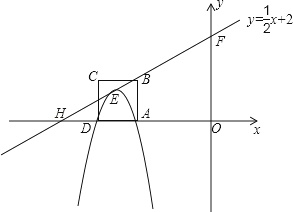
如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l:y= x+2经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线y=﹣x2+bx+c顶点E在直线l上.
x+2经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线y=﹣x2+bx+c顶点E在直线l上.
(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;
(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;
(3)设抛物线与y轴交于G点,当抛物线顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.
解:(1)∵直线l:y= x+2经过点B(x,1),
x+2经过点B(x,1),
∴1=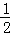 x+2,解得x=﹣2,
x+2,解得x=﹣2,
∴B(﹣2,1) ,
,
∴A(﹣2,0),D(﹣3,0),
∵抛物线经过A,D两点,
∴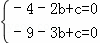 ,解得
,解得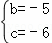 ,
,
∴抛物线经过A,D两点时的解析式为y═﹣x2﹣5x﹣6;
(2)∵顶点E(m,n)在直线l上,
∴n=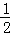 m+2,
m+2,
∴S=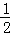 ×1×(
×1×(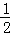 m+2)=
m+2)=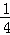 m+1,
m+1,
即S=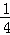 m+1(m≠4);
m+1(m≠4);
(3)如图,若以A,C,E,G为顶点的四边形能成为平行四边形,则AC=EQ,AC∥EQ,
作EH∥y轴交过Q点平行于x轴的直线相交于H,则EH⊥QH,△EHQ≌△CDA,
∴QH=AD=1,
∴E的横坐标为±1,
∵顶点E在直线l上,
∴y= ×(﹣1)+2=
×(﹣1)+2=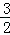 ,或y=
,或y= ×1+2=
×1+2=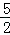
∴E(﹣1,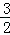 )或(1,
)或(1,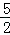 ).
).



 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
如图,已知一次函数y=x+b与反比例函数y=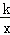 的图象交于A、B两点,其中点A的坐标为(2,3).
的图象交于A、B两点,其中点A的坐标为(2,3).
(1)求一次函数与反比例函数的解析式;
(2)求点B的坐标;
(3)请根据图象直接写出不等式x+b>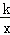 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
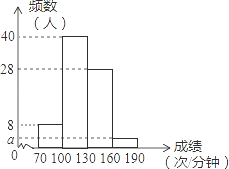
“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2﹣3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 .
(2)将跳绳次数在160~190的选手依次记为A1、A2、…An,从中随机抽取两名选手作经验交流,请用树状或列表法求恰好抽取到的选手A1和A2的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
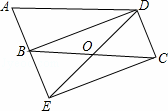
如图,将▱ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com