
分析 设A(4,t),根据三角形面积公式得到$\frac{1}{2}$•4•|t|=6,解得t=3或t=-3,则A(4,3)或(4,-3),再设直线AO的解析式为y=kx,然后把(4,3)和(4,-3)分别代入求出对应的k的值即可.
解答 解:设A(4,t),
根据题意得$\frac{1}{2}$•4•|t|=6,解得t=3或t=-3,则A(4,3)或(4,-3),
设直线AO的解析式为y=kx,
当A(4,3)时,4k=3,解得k=$\frac{3}{4}$,此时直线OA的解析式为y=$\frac{3}{4}$x,
当A(4,-3)时,4k=-3,解得k=-$\frac{3}{4}$,此时直线OA的解析式为y=-$\frac{3}{4}$x.
故答案为y=$\frac{3}{4}$x或y=-$\frac{3}{4}$x.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
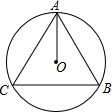 如图,△ABC的三个顶点都在圆O上,AO是∠BAC的角平分线,下列说法一定成立的是( )
如图,△ABC的三个顶点都在圆O上,AO是∠BAC的角平分线,下列说法一定成立的是( )| A. | △ABC是等腰三角形,且AC=BC | B. | △ABC是等腰三角形,且AC=AB | ||
| C. | △ABC是等腰三角形,且AB=BC | D. | △ABC是等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
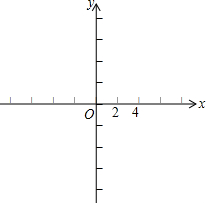 如图,在下面的平面直角坐标系中,作出以A(1,2),B(3,1),C(4,4)为顶点的三角形,并在第一象限内作出它的位似三角形A′B′C′,使原三角形与新三角形的位似比为2:1,位似中心是圆点.
如图,在下面的平面直角坐标系中,作出以A(1,2),B(3,1),C(4,4)为顶点的三角形,并在第一象限内作出它的位似三角形A′B′C′,使原三角形与新三角形的位似比为2:1,位似中心是圆点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
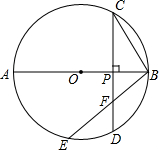 如图,⊙O的两条弦CD,BE相交于点F,AB是直径,CD⊥AB,垂足为点P,连接BC.求证:
如图,⊙O的两条弦CD,BE相交于点F,AB是直径,CD⊥AB,垂足为点P,连接BC.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com