
����Ŀ����֪��������ABCD�ı߳�Ϊ4����E�ǶԽ���BD�ӳ�����һ�㣬AE=BD������ABE�Ƶ�A˳ʱ����ת���ȣ�0�㣼����360�㣩�õ���AB��E�䣬��B��E�Ķ�Ӧ��ֱ�ΪB�䡢E�䣮
��1����ͼ1������=30��ʱ����֤��B��C=DE��
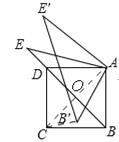
��2������B��E��DE�䣬��B��E=DE��ʱ������ͼ2�����ֵ��
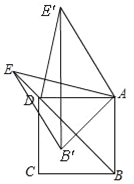
��3����ͼ3����PΪAB���е㣬��QΪ�߶�B��E��������һ�㣬��̽�����ڴ���ת�����У��߶�PQ���ȵ�ȡֵ��ΧΪ�� ����

���𰸡���1��֤����������2��45�㣨3��![]() ��PQ��4
��PQ��4![]() +2
+2
�����������������(1)������AC��B��C�����������ε����ʵó��ó�AC=AE=2OA������Rt��AOE�����ʵó���E=30�㣬Ȼ������תͼ�ε����ʵó���ADE�͡�AB��Cȫ�ȣ��Ӷ��ó��𰸣�(2)��������תͼ�ε����ʵó���AEB��͡�AE��Dȫ�ȣ��Ӷ��ó���DAE��=��EAB�䣬Ȼ������תͼ�ε����ʵó���EAE��=��BAB�䣬�Ӷ��õ���BAB��=��DAB�䣬�����ݡ�BAB��+��DAB��=90��ó��𰸣�(3)����P��PM��BE����AB=4����P��AB�е㣬����BP=2�ó�PM=![]() ������ת�����У���ABE����ת����E��BA���ӳ���ʱ����Q�͵�E�غϣ�Ȼ�����PQ�ij��ȣ��Ӷ��ó�ȡֵ��Χ.
������ת�����У���ABE����ת����E��BA���ӳ���ʱ����Q�͵�E�غϣ�Ȼ�����PQ�ij��ȣ��Ӷ��ó�ȡֵ��Χ.
�����������1����ͼ������AC��B��C�� ���ı���ABCD�������Σ�
��AB=AD��AC��BD��AC=BD=2OA����CAB=ADB=45�㣬 ��AE=BD�� ��AC=AE=2OA��
��Rt��AOE�У���AOE=90�㣬AE=2OA�� ���E=30�㣬
���DAE=��ADB����E=45�㩁30��=15�㣬 ����ת�У�AD=AB=AB���BAB��=30��
���DAE=15�㣬
�ڡ�ADE�͡�AB��C�У�  �� ���ADE�ա�AB��C����DE=B��C��
�� ���ADE�ա�AB��C����DE=B��C��
��2����ͼ��
����ת�ã�AB��=AB=AD��AE��=AE��
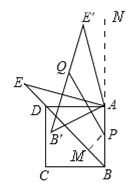
�ڡ�AEB��͡�AE��D�У� 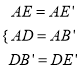 �����AEB��ա�AE��D�����DAE��=��EAB�䣬
�����AEB��ա�AE��D�����DAE��=��EAB�䣬
���EAE��=��DAB�䣬����ת�ã���EAE��=��BAB�䣬���BAB��=��DAB�䣬
�ߡ�BAB��+��DAB��=90�㣬���=��BAB��=45�㣬
��3����ͼ���ɵ㵽ֱ�ߵľ��룬����P��PM��BE����AB=4����P��AB�е㣬
��BP=2����PM=![]() ��
��
����ת�����У���ABE����ת����E��BA���ӳ���ʱ����Q�͵�E�غϣ�
��AQ=AE=BQ=4![]() ��PQ=AQ+AP=4
��PQ=AQ+AP=4![]() +2��
+2��
�ʴ�Ϊ![]() ��PQ��4
��PQ��4![]() +2��
+2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD�У���A1 �� A2 �� A3 �� A4��C1 �� C2 �� C3 �� C4�ֱ�AB��CD����ȷֵ㣬��B1 �� B2��D1 �� D2�ֱ���BC��DA�����ȷֵ㣬��֪�ı���A4B2C4D2�����Ϊ1����ƽ���ı���ABCD���Ϊ��������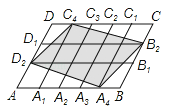
A.2
B.![]()
C.![]()
D.15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ab��(a2b��ab��ab2)��ab������a��b����Ϊ�㣬��2(34)��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���人ij�춬�����������9����������©�3������һ���人������±�������¸ߣ�������
A. 12�� B. ��12�� C. 6�� D. ��6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��1����=10��9�ף���50�����ÿ�ѧ��������ʾΪ�� ��
A. 50��10��9��B. 5��10��9��C. 0.5��10��9��D. 5��10��8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�涨ѧ����ѧ����ѧ�ɼ�����Ϊ100�֣�����ƽʱѧϰ�ɼ�ռ30%����ĩ����ɼ�ռ70%��С��������ɼ����ٷ��ƣ�������80�֣�90�֣���С����ѧ�ڵ���ѧ�ɼ��ǣ�������
A. 83��B. 86��C. 87��D. 92.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ÿСʱ����38��������ڹ涨ʱ���ڻ���15��������ɣ���ÿСʱ����42�����������Գ������5�����ʣ��涨ʱ���Ƕ��٣���涨ʱ��ΪxСʱ������з���Ϊ��������
A. 38x��15=42x+5 B. 38x+15=42x��5 C. 42x+38x=15+5 D. 42x��38x=15��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
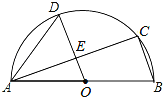
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��OD��BC��OD��AC���ڵ�E��
��1������B=72��������CAD�Ķ�����
��2����AB=13��AC=12����DE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com