练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

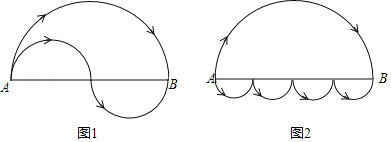
    【题目】黑蚂蚁沿着大半圆从A地爬到B地，白蚂蚁沿着两个小半圆弧路线也从A地爬到B地．它们同时从A地出发，让人奇怪的是，两只蚂蚁同时爬到B地．假设AB＝a

    （1）请你帮忙裁决，两只蚂蚁谁爬得快？

    （2）两只蚂蚁对你的裁决很不满意，决定到图2中的比赛场地再比一次，依然黑蚂蚁沿着大半圆爬，白蚂蚁沿着小半圆爬，同时从A地出发，那么请问哪只蚂蚁先爬到B地？说明理由．

    【答案】（1）两只蚂蚁爬的一样快；（2）两只蚂蚁同时到达，理由详见解析．

    【解析】

    （1）黑蚂蚁的爬行路线是半个大圆，长度为大圆周长一半，白蚂蚁是一个小圆的周长；

    （2）黑蚂蚁的爬行路线是半个大圆，长度为大圆周长一半，白蚂蚁是两个小圆的周长．

    解：（1）黑蚂蚁爬行路程：πa；白蚂蚁的爬行路程：πa；

    ∴两只蚂蚁爬的一样快；

    （2）两只蚂蚁同时到达．

    理由如下：

    黑蚂蚁的爬行路程：πa；白蚂蚁的爬行路程：2×π×＝πa；

    ∴两只蚂蚁同时到达．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校准备组织师生共60人，从南靖乘动车前往厦门参加夏令营活动，动车票价格如表所示：（教师按成人票价购买，学生按学生票价购买）．

    运行区间

    成人票价（元/张）

    学生票价（元/张）

    出发站

    终点站

    一等座

    二等座

    二等座

    南靖

    厦门

    26

    22

    16

    若师生均购买二等座票，则共需1020元．

    （1）参加活动的教师和学生各有多少人?

    （2）由于部分教师需提早前往做准备工作，这部分教师均购买一等座票，而后续前往的教师和学生均购买二等座票．设提早前往的教师有x人，购买一、二等座票全部费用为y元．

    ①求y关于x的函数关系式；

    ②若购买一、二等座票全部费用不多于1032元，则提早前往的教师最多只能多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

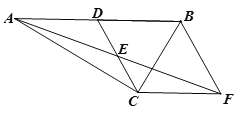
    【题目】已知：如图，在Rt△ACB中，∠ACB=90°，点D是AB的中点，点E是CD的中点，过点C作CF∥AB叫AE的延长线于点F．

    （1）求证：△ADE≌△FCE；

    （2）若∠DCF=120°，DE=2，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学决定在本校学生中，开展足球、篮球、羽毛球、乒乓球四种活动，为了了解学生对这四种活动的喜爱情况，学校随机调查了该校名学生，看他们喜爱哪一种活动（每名学生必选一种且只能从这四种活动中选择一种），现将调查的结果绘制成如下不完整的统计图．

    （1）=________，=_________；

    （2）请补全图中的条形图；

    （3）在抽查的名学生中，喜爱打乒乓球的有10名同学（其中有4名女生，包括小红、小梅），现将喜爱打乒乓球的同学平均分成两组进行训练，且女生每组分两人，求小红、小梅能分在同一组的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，数轴上A、B两点表示的数分别为a、b，且a、b满足|a＋2|＋(b－8)2＝0，点P从点A出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动．设运动时间为t秒（t＞0）

    (1) ① 线段AB的中点表示的数为___________

    ② 用含t的代数式表示：t秒后，点P表示的数为___________

    (2) 求当t为何值时，PQ＝AB

    (3) 若点M为PA的中点，点N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC与Rt△ABD中，，，AC、BD相交于点G，过点A作交CB的延长线于点E，过点B作交DA的延长线于点F，AE、BF相交于点H．

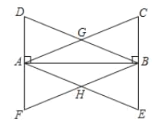
    （1）证明：ΔABD≌△BAC．

    （2）证明：四边形AHBG是菱形．

    （3）若AB=BC，证明四边形AHBG是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：抛物线y=x2+bx+c经过点（2，-3）和（4，5）。

    （1）求抛物线的表达式及顶点坐标；

    （2）将抛物线沿x轴翻折，得到图象G，求图象G的表达式；

    （3）在（2）的条件下，当-2<x<2时，直线y=m与该图象有一个公共点，求m的值或取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在△ABC中，∠BAC=90°，AB=AC，点E在AC上（且不与点A，C重合），在△ABC的外部作△CED，使∠CED=90°，DE=CE，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．

    （1）请直接写出线段AF，AE的数量关系 ；

    （2）将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；

    （3）在图②的基础上，将△CED绕点C继续逆时针旋转，请判断（2）问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=3x与反比例函数y=（k≠0）的图象交于A（1，m）和点B．

    （1）求m，k的值，并直接写出点B的坐标；

    （2）过点P（t，0）（-1≤t≤1）作x轴的垂线分别交直线y=3x与反比函数y=（k≠0）的图象于点E，F．

    ①当t=时，求线段EF的长；

    ②若0＜EF≤8，请根据图象直接写出t的取值范围．

    查看答案和解析>>

    同步练习册答案