Question

11．如图，正方形ABCD的面积为5，点M，N，P分别是边BC，CD和对角线BD上的动点，则PM+PN的最小值为$\sqrt{5}$．

Answer 1

分析 在AB上取BN′=BN，连结PN′，先证明△PNB≌PN′B，则NP=PN′，然后将MP+PN转化为PM+PN′，当点N、P、M在一条直线上且MN⊥DC时，MP+PN有最小值，最小值等于正方形的边长．

解答 解：在AB上取BN′=BN，连结PN′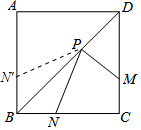

∵ABCD为正方形，
∴∠ABD=∠CBD=45°．
在△PNB和PN′B中$\left\{\begin{array}{l}{BN′=NB}\\{∠NBP=∠N′BP}\\{BP=BP}\end{array}\right.$，
∴△PNB≌PN′B．
∴NP=PN′．
∴MP+PN=PM+PN′．
当点N、P、M在一条直线上且MN⊥DC时，MP+PN有最小值，最小值等于正方形的边长=$\sqrt{5}$．
故答案为：$\sqrt{5}$．

点评 本题主要考查的是轴对称路径最短、正方形的性质、垂线段的性质，熟练将将MP+PN转化为PM+PN′是解题的关键．