
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是( )
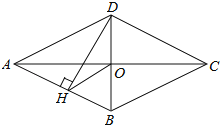
A.20°B.25°C.30°D.40°
【答案】A
【解析】
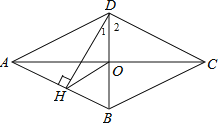
先根据菱形的性质得OD=OB,AB∥CD,BD⊥AC,则利用DH⊥AB得到DH⊥CD,∠DHB=90°,所以OH为Rt△DHB的斜边DB上的中线,得到OH=OD=OB,利用等腰三角形的性质得∠1=∠DHO,然后利用等角的余角相等即可求出∠DHO的度数.
解:∵四边形ABCD是菱形,
∴OD=OB,AB∥CD,BD⊥AC,
∵DH⊥AB,
∴DH⊥CD,∠DHB=90°,
∴OH为Rt△DHB的斜边DB上的中线,
∴OH=OD=OB,
∴∠1=∠DHO,
∵DH⊥CD,
∴∠1+∠2=90°,
∵BD⊥AC,
∴∠2+∠DCO=90°,
∴∠1=∠DCO,
∴∠DHO=∠DCA,
∵四边形ABCD是菱形,
∴DA=DC,
∴∠CAD=∠DCA=20°,
∴∠DHO=20°,
故选A.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠DAE=∠E,∠B=∠D,试说明AB与DC平行.

解:因为∠DAE=∠E,(已知)
所以____∥____(_______)
所以∠D=____(_______)
因为∠B=∠D,(已知)
所以∠B=∠____(_______)
所以____∥____(_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为![]() BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
![]()
A. 点E B. 点F C. 点M D. 点N
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1)(1,1),(1,2),(2,2)……根据这个规律,第2019个点的坐标为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意两个数![]() 、
、![]() 的大小比较,有下面的方法:当
的大小比较,有下面的方法:当![]() 时,一定有
时,一定有![]() ;当
;当![]() 时,一定有
时,一定有![]() ;当
;当![]() 时,一定有
时,一定有![]() .反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:
.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:
(1)已知:![]() ,
,![]() ,且
,且![]() ,试判断
,试判断![]() 的符号;
的符号;
(2)已知:![]() 、
、![]() 、
、![]() 为三角形的三边,比较
为三角形的三边,比较![]() 和
和![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD被直线BD,DF所截,AB∥CD,BFBD,垂足为B,EG平分BED,CDE50,F25.
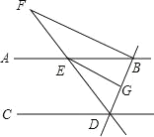
⑴求证:EG∥BF;⑵求BDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com