
【题目】如图,直线AB,CD被直线BD,DF所截,AB∥CD,BFBD,垂足为B,EG平分BED,CDE50,F25.
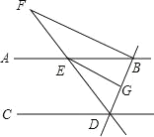
⑴求证:EG∥BF;⑵求BDC的度数.
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=20°,则∠DHO的度数是( )
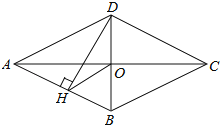
A.20°B.25°C.30°D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB,E、F、G、H分别是AB,BC,CD,AD边上的点,EG⊥FH,FH=2![]() ,则四边形EFGH的面积为( )
,则四边形EFGH的面积为( )
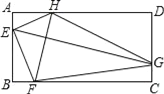
A. 6![]() B. 12 C. 12
B. 12 C. 12![]() D. 24
D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,点P和点Q是直线BD上不重合的两个动点,AP∥CQ,AD=BD.
(1)如图①,求证:BP+BQ=BC;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若DQ=2,DP=6,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如表所示
型 号 | A | B | C |
进价(元/套) | 40 | 55 | 50 |
售价(元/套) | 50 | 80 | 65 |
(1)用含x、y的代数式表示购进C种玩具的套数;
(2)求y与x之间的函数关系式;
(3)假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.
①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 平行线
平行线![]() 与
与![]() 与
与![]() 与
与![]() 之间的距离分别为
之间的距离分别为![]() 且
且![]()
![]() ,
,![]() .我们把四个顶点分别在
.我们把四个顶点分别在![]() 这四条平行线上的四边形称为“线上四边形”
这四条平行线上的四边形称为“线上四边形”
(1)如图1,正方形![]() 为“线上四边形”,
为“线上四边形”,![]() 于点
于点![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .求正方形
.求正方形![]() 的边长.
的边长.

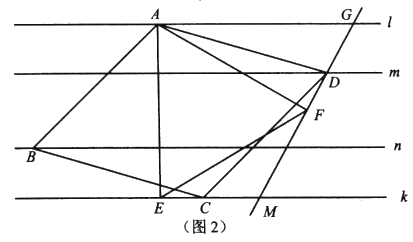
(2)如图2,菱形![]() 为“线上四边形”且
为“线上四边形”且![]() 是等边三角形,点
是等边三角形,点![]() 在直线
在直线![]() 上,连接
上,连接![]() 且
且![]() 的延长线分别交直线
的延长线分别交直线![]() 于点
于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应点之间的距离.这个结论可以推广为:
对应点之间的距离.这个结论可以推广为:![]() 表示在数轴上数
表示在数轴上数![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 点的对应数为
点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,解决下列问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)若数轴上表示![]() 的点在
的点在![]() 与
与![]() 之间,则
之间,则![]() 的值为_________;
的值为_________;
(4)当![]() 满足_________时,则
满足_________时,则![]() 的值最小,最小值是_________.
的值最小,最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
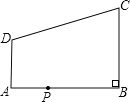
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(4,0),B(2,0),若点C在一次函数y=![]() x+2的图象上,且△ABC为直角三角形,则满足条件的点C有( )
x+2的图象上,且△ABC为直角三角形,则满足条件的点C有( )
A.4个B.2个C.3个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com