
【题目】在ABCD中,点P和点Q是直线BD上不重合的两个动点,AP∥CQ,AD=BD.
(1)如图①,求证:BP+BQ=BC;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若DQ=2,DP=6,则BC= .

【答案】(1)证明见解析(2)证明见解析(3)BC=4或8
【解析】(1)根据平行四边形的性质证明△ADP≌△CBQ,得BQ=PD,由AD=BD=BC得:BC=BD=BP+PD=BP+BQ;
(2)图②,证明△ABP≌△CDQ,得PB=DQ,根据线段的和得结论;
图③,证明△ADP≌△CBQ,得PD=BQ,同理得出结论;
(3)分别代入图①和图②条件下的BC,计算即可.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∴∠ADB=∠CBD,
∵AP∥CQ,∴∠APQ=∠CQB,∴△ADP≌△CBQ,
∴DP=BQ,∵AD=BD,AD=BC,∴BD=BC,∵BD=BP+DP,∴BC=BP+BQ;
(2)图②:BQ﹣BP=BC,理由是:∵AP∥CQ,∴∠APB=∠CQD,
∵AB∥CD,∴∠ABD=∠CDB,∴∠ABP=∠CDQ,∵AB=CD,∴△ABP≌△CDQ,
∴BP=DQ,∴BC=AD=BD=BQ﹣DQ=BQ﹣BP;
图③:BP﹣BQ=BC,理由是:同理得:△ADP≌△CBQ,∴PD=BQ,
∴BC=AD=BD=BP﹣PD=BP﹣BQ;
(3)图①,BC=BP+BQ=DQ+PD=2+6=8,图②,BC=BQ﹣BP=PD﹣DQ=6﹣2=4,∴BC=4或8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】分别以△ABC的各边为一边向三角形外部作正方形,若这三个正方形的面积分别为6cm2、8cm2、10cm2,则△ABC_____直角三角形.(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
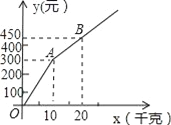
【题目】甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克_____元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,若某人想在“五一期间”采摘樱桃25千克,那么甲、乙哪个采摘园较为优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=a有实数根x1、x2,且x1≠x2,有下列结论:①x1=2,x2=3 ②a>-![]() ③二次函数
③二次函数![]() 的图象与x轴交点坐标为(2,0),(3,0),其中正确的结论的个数是( )
的图象与x轴交点坐标为(2,0),(3,0),其中正确的结论的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红各自随机选择本周日的上午或下午去扬州科技馆参观.
(1) 小明、小刚本周日的上午去参观的概率为_____;
(2) 求他们三人在同一半天去参观的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com