
【题目】“六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如表所示
型 号 | A | B | C |
进价(元/套) | 40 | 55 | 50 |
售价(元/套) | 50 | 80 | 65 |
(1)用含x、y的代数式表示购进C种玩具的套数;
(2)求y与x之间的函数关系式;
(3)假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.
①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套.
【答案】当x取最大值23时,P有最大值,最大值为595元.此时购进A、B、C种玩具分别为23套、16套、11套.
【解析】试题分析:
(1)利用三种玩具的总和是50套可求解;
(2)结合总费用是2350列方程可得y与x之间的函数关系式;
(3)①根据利润=销售收入﹣进价﹣其它费用列出p与x之间的函数关系式;
②根据题意确定自变量x的取值范围,由一次函数的性质可得到最大值,从而求解.
解:(1)已知共购进A、B、C三种新型的电动玩具共50套,故购进C种玩具套数为:50﹣x﹣y;
(2)由题意得40x+55y+50(50﹣x﹣y)=2350,整理得y=2x﹣30;
(3)①利润=销售收入﹣进价﹣其它费用,
故:p=(50﹣40)x+(80﹣55)y+(65﹣50)(50﹣x﹣y)﹣200,
又∵y=2x﹣30,
∴整理得p=15x+250,
②购进C种电动玩具的套数为:50﹣x﹣y=50﹣x﹣(2x﹣30)=80﹣3x,
据题意列不等式组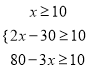 ,解得20≤x≤
,解得20≤x≤![]() ,
,
∴x的范围为20≤x≤![]() ,且x为整数,故x的最大值是23,
,且x为整数,故x的最大值是23,
∵在p=15x+250中,k=15>0,
∴P随x的增大而增大,
∴当x取最大值23时,P有最大值,最大值为595元.此时购进A、B、C种玩具分别为23套、16套、11套.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1)(1,1),(1,2),(2,2)……根据这个规律,第2019个点的坐标为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.

(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.

(1)求证:DF是⊙O的切线;
(2)若CF=2,DF=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B﹣C﹣D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD被直线BD,DF所截,AB∥CD,BFBD,垂足为B,EG平分BED,CDE50,F25.
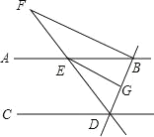
⑴求证:EG∥BF;⑵求BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 以每秒
以每秒![]() 个单位的速度向点
个单位的速度向点![]() 方向运动,连接
方向运动,连接![]() ,把
,把![]() 沿
沿![]() 翻折,得到
翻折,得到![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() .
.

(1)若![]() ,当
,当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的值;
的值;
(2)若点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,求
,求![]() 的值;
的值;
(3)若![]() 的最小值为
的最小值为![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60(![]() +3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
+3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
(1)分别求出AC,BC(结果保留根号)
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监船沿AC前往C处盘看,图中有无触礁的危险?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com