
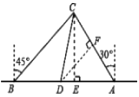
【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60(![]() +3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
+3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
(1)分别求出AC,BC(结果保留根号)
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监船沿AC前往C处盘看,图中有无触礁的危险?请说明理由.

【答案】A与C的距离为120![]() 海里,B与C的距离为180
海里,B与C的距离为180![]() 海里;(2)无触礁危险.
海里;(2)无触礁危险.
【解析】试题分析:(1)、过点C作CE⊥AB于点E,可得∠CBD=45°,∠CAD=60°,设CE=x,根据Rt△CAE的三角函数得出AE= ![]() ,最后根据AB=BE+AE求出x的值,最后根据直角三角形的三角函数求出答案;(2)、过点D作DF⊥AC于点F,根据Rt△ADF的三角函数求出DF的长度,然后与80进行比较大小,从而得出答案.
,最后根据AB=BE+AE求出x的值,最后根据直角三角形的三角函数求出答案;(2)、过点D作DF⊥AC于点F,根据Rt△ADF的三角函数求出DF的长度,然后与80进行比较大小,从而得出答案.
试题解析:(1)、如图所示,过点C作CE⊥AB于点E,可得∠CBD=45°,∠CAD=60°,
设CE=x,在Rt△CBE中,BE=CE=x,
在Rt△CAE中, ![]() ,即AE=CE·tan30°,∴AE=
,即AE=CE·tan30°,∴AE= ![]()
∵AB=60(![]() +3)海里,∴AB=BE+AE=x+
+3)海里,∴AB=BE+AE=x+ ![]() =60(
=60(![]() ),即x=180海里,
),即x=180海里,
则AC=![]() 海里, BC=
海里, BC=![]() x=180
x=180![]() 海里;
海里;
答:A与C的距离为120![]() 海里,B与C的距离为180
海里,B与C的距离为180![]() 海里;
海里;
(2)、无触礁危险.
如图所示,过点D作DF⊥AC于点F,在△ADF中,∵AD=100,∠CAD=60°,∴DF=ADsin60°=50![]() ≈86.6>80,故海监船沿AC前往C处盘查,无触礁危险.
≈86.6>80,故海监船沿AC前往C处盘查,无触礁危险.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”前夕,某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如表所示
型 号 | A | B | C |
进价(元/套) | 40 | 55 | 50 |
售价(元/套) | 50 | 80 | 65 |
(1)用含x、y的代数式表示购进C种玩具的套数;
(2)求y与x之间的函数关系式;
(3)假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.
①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说,
,也就是说,![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应点之间的距离.这个结论可以推广为:
对应点之间的距离.这个结论可以推广为:![]() 表示在数轴上数
表示在数轴上数![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例![]() 已知
已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 点的对应数为
点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,解决下列问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,求
,求![]() 的值;
的值;
(3)若数轴上表示![]() 的点在
的点在![]() 与
与![]() 之间,则
之间,则![]() 的值为_________;
的值为_________;
(4)当![]() 满足_________时,则
满足_________时,则![]() 的值最小,最小值是_________.
的值最小,最小值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式,两项成绩的原始分均为100分,前6名选手的得分如下:

根据规定,笔试成绩和面试成绩按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)
(1)这6名选手笔试成绩的平均数是_____分,中位数是_____分,众数是______分.
(2)现已知1号选手的综合成绩为88分,求笔试成绩和面试成绩的百分比各为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
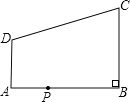
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(发现)如图1,在![]() 中,
中,![]() 分别交
分别交![]() 于
于![]() ,交
,交![]() 于
于![]() .已知
.已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
思考发现,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,构造
,构造![]() ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).

请回答:![]() 的值为______.
的值为______.
(2)(应用)如图3,在四边形![]() 中,
中,![]() ,
,![]() 与
与![]() 不平行且
不平行且![]() ,对角线
,对角线![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)(拓展)如图4,已知平行四边形![]() 和矩形
和矩形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,
,![]() ,判断
,判断![]() 与
与![]() 的数量关系并证明.
的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,AOBC的顶点A、C的坐标分别为A(﹣2,0)、C(0,3),反比例函数的图象经过点B.
(1)求反比例函数的表达式;
(2)这个反比例函数的图象与一个一次函数的图象交于点B、D(m,1),根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com