
【题目】问题发现
(1)如图1,![]() 和
和![]() 均为等边三角形,点D在边BC上,连接CE.求证:
均为等边三角形,点D在边BC上,连接CE.求证:![]() .
.
拓展探究
(2)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点D在边BC上,连接CE
,点D在边BC上,连接CE
ⅰ)求![]() 的度数;
的度数;
ⅱ)请判断线段AC、CD、CE之间的数量关系,并说明理由.
解决问题
(3)如图3,在四边形ABCD中,![]() ,
,![]() ,
,![]() ,AC与BD交于点E,求出线段AC的长度.
,AC与BD交于点E,求出线段AC的长度.

【答案】(1)见解析;(2)i)![]() ,ⅱ)
,ⅱ)![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)根据SAS可证明△BAD≌△CAE,可得结论;
(2)i)先证明△ABD≌△ACE,得∠ACE=∠B=45°;
ⅱ)由△ABD≌△ACE,得BD=CE,利用等边三角形的AC=BC=BD+DC等量代换可得结论;
(3)过点A作AC的垂线,交CB的延长线于点F,证明△ACF是等腰直角三角形,则利用(2)的结论求AC的长.
(1)∵![]() 和
和![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)i)![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ;
;
ⅱ)![]() ;
;
理由:由ⅰ)得![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵在等腰![]() 中,
中,![]() ,
,
∴![]() ;
;
(3)如解图,过点A作AC的垂线,交CB的延长线于点F,
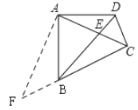
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴A、B、C、D四点共圆,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
由(2)得![]() ,
,
∴![]() .
.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】小李准备进行如下的操作,把一根长![]() 的铁丝剪成两段,并把每段首尾相连各围成一个长宽不等的矩形,两矩形相似且相似比为
的铁丝剪成两段,并把每段首尾相连各围成一个长宽不等的矩形,两矩形相似且相似比为![]() .
.
(1)要使这两个矩形的面积之和为![]() ,较小矩形的长宽各是多少?
,较小矩形的长宽各是多少?
(2)小李认为这两个矩形的面积和不可能为![]() ,你同意吗?说明理由.(说明:相似多边形的周长比等于相似比,面积比等于相似比的平方)
,你同意吗?说明理由.(说明:相似多边形的周长比等于相似比,面积比等于相似比的平方)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在y轴,x轴上,点B的坐标为![]() ,直线
,直线![]() 分别交AB,BC于点M,N,
分别交AB,BC于点M,N,![]() ,反比例函数
,反比例函数![]() 图象经过点M,N.
图象经过点M,N.
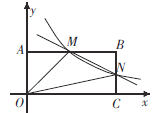
(1)求反比例函数的表达式;
(2)根据图象,请直接写出不等式![]() 的解集________.
的解集________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)如图2,连接BC,PB,PC,设△PBC的面积为S.
①求S关于t的函数表达式;
②求P点到直线BC的距离的最大值,并求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上.下列结论:①BD是∠ABE的平分线;②AB⊥AC;③∠C=30°;④线段DE是△BDC的中线;⑤AD+BD=AC.其中正确的有( )个.

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图: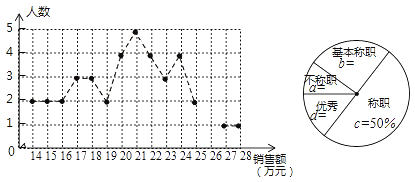
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当 ![]() 时为“基本称职”,当
时为“基本称职”,当![]() 时为“称职”,当
时为“称职”,当![]() 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=-x2+2![]() x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+
x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+![]() AP的最小值为( ).
AP的最小值为( ).
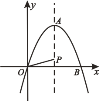
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品生产基地共有5条生产线,每条生产线每月生产药品20万盒,该基地打算从第一个月开始到第五个月结束,对每条生产线进行升级改造.改造时,每个月只升级改造一条生产线,这条生产线当月停产,并于下个月投入生产,其他生产线则正常生产.经调查,每条生产线升级改造后,每月的产量会比原来提高20%.
(1)根据题意,完成下面问题:
①把下表补充完整(直接写在横线上):
月数 | 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 | … |
产量/万盒 |
|
|
| 92 | … | … | … |
②从第1个月进行升级改造后,第 个月的产量开始超过未升级改造时的产量;
(2)若该基地第x个月(1≤x≤5,且x是整数)的产量为y万盒,求y关于x的函数关系式;
(3)已知每条生产线的升级改造费是30万元,每盒药品可获利3元.设从第1个月开始升级改造后,生产药品所获总利润为W1万元;同时期内,不升级改造所获总利润为W2万元设至少到第n个月(n为正整数)时,W1大于W2,求n的值.(利润=获利﹣改造费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com