
分析 根据分式的乘方,可得分式的乘除法,根据分式的乘除法,做乘法运算时要注意先把分子、分母能因式分解的先分解,然后约分.
解答 解:原式=xn+1÷($\frac{{x}^{n}}{{y}^{2n}}$)•(-$\frac{{x}^{4}}{{y}^{4}}$)
=-xn+1•$\frac{{y}^{2n}}{{x}^{n}}$•$\frac{{x}^{4}}{{y}^{4}}$
=-x5y2n-4,
故答案为:-x5y2n-4.
点评 本题考查了分式的乘除法,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
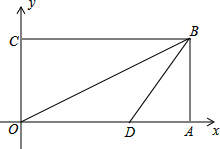 如图,在平面直角坐标系中,点O是坐标原点,四边形OABC为矩形,OA边在x轴上,OC边在y轴上.OB是矩形的对角线,点B的坐标是(8,4),点D在OA上,tan∠ABD=$\frac{3}{4}$.
如图,在平面直角坐标系中,点O是坐标原点,四边形OABC为矩形,OA边在x轴上,OC边在y轴上.OB是矩形的对角线,点B的坐标是(8,4),点D在OA上,tan∠ABD=$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com