
分析 (1)根据等式的性质,可化简方程,根据描点法,可画出相应函数图象,根据函数与方程的关系,可得答案;
(2)根据等式的性质,可化简方程,根据描点法,可画出相应函数图象,根据函数与方程的关系,可得答案.
解答 解:(1)-2x+3=5,化简,得
x+1=0.
在平面直角坐标系中画函数y=x+1的图象,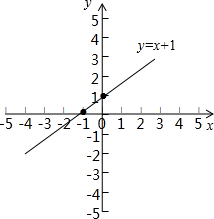 ,
,
由函数图象与x轴的交点坐标(-1,0),得
方程-2x+3=5的解是x=-1;
(2)2x-1=3,化简,得
x-2=0.
在平面直角坐标系中画函数y=x-2的图象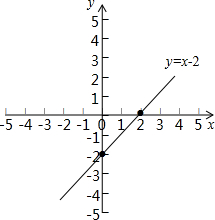 ,
,
由函数图象与x轴的交点坐标(2,0),得
方程2x-1=3的解是x=2.
点评 本题考查了一次函数与一元一次方程,利用了一次函数的图象与x轴交点的横坐标的实质就是解一元一次方程.即“形”题用“数”解,“数”题用“形”解,充分体现了数形结合的思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
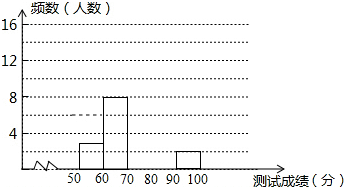 为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 3 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 13 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
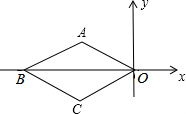 如图,菱形ABCO中AO=$\sqrt{3}$,∠AOC=60°,点M第一次从点O移动到点A,第二次从点A移动到点B,第三次从点B移动到点C,第四次从点C移动到点O…照此移动规律,点M第39次移动到的点的坐标是(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
如图,菱形ABCO中AO=$\sqrt{3}$,∠AOC=60°,点M第一次从点O移动到点A,第二次从点A移动到点B,第三次从点B移动到点C,第四次从点C移动到点O…照此移动规律,点M第39次移动到的点的坐标是(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 6 | 5 | 5 |
| A. | 3,3 | B. | 3,3.5 | C. | 3.5,3.5 | D. | 3.5,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 月用水量(吨) | 3 | 4 | 5 | 8 |
| 户数 | 2 | 3 | 5 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
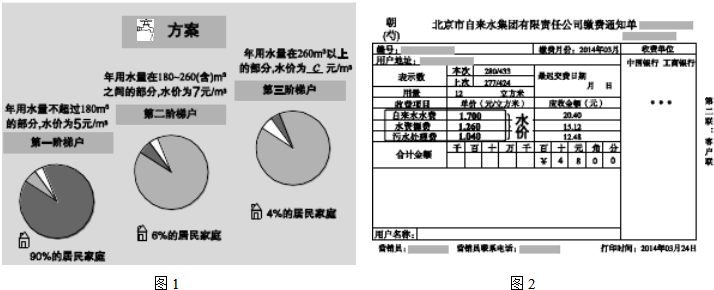
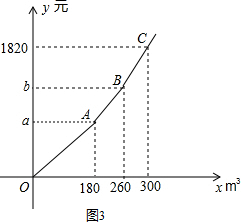
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com