
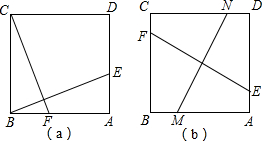
 已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF;
已知正方形ABCD,点E、F分别是AD、AB边上的点,且BE⊥CF; ,
,
|

|


科目:初中数学 来源: 题型:
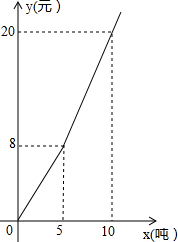 随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:
随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
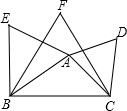 如图,根据图形解答下列问题
如图,根据图形解答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
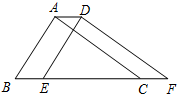 如图,将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF.
如图,将周长为8,面积为s的△ABC沿BC方向平移1个单位得到△DEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com