
【题目】已知直线l1∥l2 , 直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点 
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
【答案】
(1)解:∠APB=∠PAC+∠PBD,
如图1,过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∴∠APE+∠BPE=∠PAC+∠PBD,
∴∠APB=∠PAC+∠PBD;
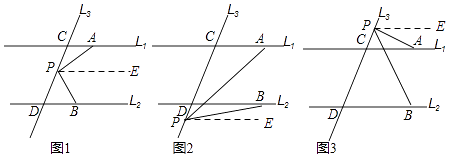
(2)解:不成立,
如图2:∠PAC=∠APB+∠PBD,
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APB=∠APE﹣∠BPE=∠PAC﹣∠PBD,
∴∠PAC=∠APB+∠PBD;
如图3:∠PBD=∠PAC+∠APB,
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵APB=∠BPE﹣∠APE=∠PBD﹣∠PAC,
∴∠PBD=∠PAC+∠APB.
【解析】(1)过点P作PE∥l1 , 根据平行线的性质即可得到,∠APE=∠PAC,∠BPE=∠PBD,根据∠APE+∠BPE=∠PAC+∠PBD,可得∠APB=∠PAC+∠PBD;(2)根据(1)的方法,过点P作PE∥l1 , 根据平行线的性质,可得∠APE=∠PAC,∠PBD=∠BPE,图2中根据∠APB=∠APE﹣∠BPE,可得∠PAC=∠APB+∠PBD;图3中,根据∠APB=∠BPE﹣∠APE,可得∠PBD=∠PAC+∠APB.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补).


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】填写推理理由: 如图,CD∥EF,∠1=∠2,求证:∠3=∠ACB.
证明:∵CD∥EF,
∴∠DCB=∠2 ![]()
∵∠1=∠2,∴∠DCB=∠1. ![]()
∴GD∥CB ![]() .
.
∴∠3=∠ACB ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并补充下面推理过程: 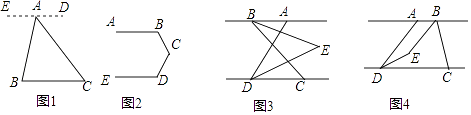
(1)如图1,已知点A是BC外一点,连接AB,AC.求∠BAC+∠B+∠C的度数. 解:过点A作ED∥BC,所以∠B= ![]() ,∠C=
,∠C= ![]() .
.
又因为∠EAB+∠BAC+∠DAC=180°.
所以∠B+∠BAC+∠C=180°.
(2)如图2,已知AB∥ED,求∠B+∠BCD+∠D的度数.
(3)已知AB∥CD,点C在点D的右侧,∠ADC=70°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间. Ⅰ.如图3,点B在点A的左侧,若∠ABC=60°,则∠BED的度数为 ![]() °.
°.
Ⅱ.如图4,点B在点A的右侧,且AB<CD,AD<BC.若∠ABC=n°,则∠BED的度数为 ![]() °.(用含n的代数式表示)
°.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式乘法中不能用平方差公式计算的是( )
A.(2x2y﹣1)(﹣2x2﹣1)
B.(a3﹣b3)(b3﹣a3)
C.(a+b)(a﹣b)
D.(a2+b2)(b2﹣a2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com