
����Ŀ���Ķ������������������̣� 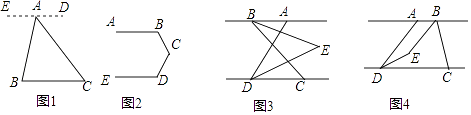
��1����ͼ1����֪��A��BC��һ�㣬����AB��AC�����BAC+��B+��C�Ķ����� �⣺����A��ED��BC�����ԡ�B= ![]() ����C=
����C= ![]() ��
��
����Ϊ��EAB+��BAC+��DAC=180�㣮
���ԡ�B+��BAC+��C=180�㣮
��2����ͼ2����֪AB��ED�����B+��BCD+��D�Ķ�����
��3����֪AB��CD����C�ڵ�D���Ҳ࣬��ADC=70�㣬BEƽ�֡�ABC��DEƽ�֡�ADC��BE��DE���ڵ�ֱ�߽��ڵ�E����E��AB��CD����ƽ����֮�䣮 ����ͼ3����B�ڵ�A����࣬����ABC=60�㣬���BED�Ķ���Ϊ ![]() �㣮
�㣮
����ͼ4����B�ڵ�A���Ҳ࣬��AB��CD��AD��BC������ABC=n�㣬���BED�Ķ���Ϊ ![]() �㣮���ú�n�Ĵ���ʽ��ʾ��
�㣮���ú�n�Ĵ���ʽ��ʾ��
���𰸡�
��1���⣺��ED��BC�����B=��EAD����C=��DAE��
�ʴ�Ϊ����EAD����DAE��
��2���⣺��C��CF��AB��
��AB��DE��
��CF��DE��
���D=��FCD��
��CF��AB��
���B=��BCF��
�ߡ�BCF+��BCD+��DCF=360�㣬
���B+��BCD+��D=360�㣬
��3������ͼ2������E��EF��AB��
��AB��CD��
��AB��CD��EF��
���ABE=��BEF����CDE=��DEF��
��BEƽ�֡�ABC��DEƽ�֡�ADC����ABC=60�㣬��ADC=70�㣬
���ABE= ![]() ��ABC=30�㣬��CDE=
��ABC=30�㣬��CDE= ![]() ��ADC=35�㣬
��ADC=35�㣬
���BED=��BEF+��DEF=30��+35��=65�㣻
�ʴ�Ϊ��65��
����ͼ3������E��EF��AB��
��BEƽ�֡�ABC��DEƽ�֡�ADC����ABC=n�㣬��ADC=70��
���ABE= ![]() ��ABC=
��ABC= ![]() n�㣬��CDE=
n�㣬��CDE= ![]() ��ADC=35��
��ADC=35��
��AB��CD��
��AB��CD��EF��
���BEF=180�㩁��ABE=180�㩁 ![]() n�㣬��CDE=��DEF=35�㣬
n�㣬��CDE=��DEF=35�㣬
���BED=��BEF+��DEF=180�㩁 ![]() n��+35��=215�㩁
n��+35��=215�㩁 ![]() n�㣮
n�㣮
�ʴ�Ϊ��215�㩁 ![]() n��
n��
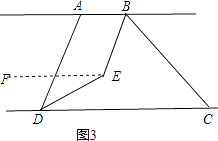
����������1������ƽ���ߵ����ʼ��ɵõ����ۣ���2����C��CF��AB����ƽ���ߵ����ʵõ���D=��FCD����B=��BCF��Ȼ�������֪�������ɵõ����ۣ���3������E��EF��AB��Ȼ�������ֱ��ƽ���ڴ�����ȣ��������BED�Ķ����� ��BED�Ķ����ı䣮����E��EF��AB�����ɽ�ƽ���ߵĶ���ɵã���ABE= ![]() ��ABC=
��ABC= ![]() n�㣬��CDE=
n�㣬��CDE= ![]() ��ADC=35�㣬Ȼ�������ֱ��ƽ���ڴ�����ȼ�ͬ���ڽǻ����ɵã���BEF=180�㩁��ABE=180�㩁
��ADC=35�㣬Ȼ�������ֱ��ƽ���ڴ�����ȼ�ͬ���ڽǻ����ɵã���BEF=180�㩁��ABE=180�㩁 ![]() n�㣬��CDE=��DEF=35�㣬���������BED=��BEF+��DEF=180�㩁
n�㣬��CDE=��DEF=35�㣬���������BED=��BEF+��DEF=180�㩁 ![]() n��+35��=215�㩁
n��+35��=215�㩁 ![]() n�㣮
n�㣮
�����㾫��������ƽ���ߵ������ǽ����ĸ�������Ҫ֪����ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y��ax2��bx+5��a��5����ͼ����x�ύ�ڣ�1��0������b��a+2015��ֵ��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A. 4������ƽ�����ǡ�2 B. ����һ��û��ƽ����
C. ƽ��������������������0��1 D. 0.9������ƽ������0.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˳������һ���ı��εĸ����е㣬�õ�һ�����Σ��������ı����У���ƽ���ı��Σ������Σ��۾��Σ��ܶԽ����ഹֱ���ı��Σ������������ı�����______��������Ϊ��ȷ��������ں����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=6����E�ڱ�CD�ϣ���CE=2DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ�����ABG�ա�AFG����BG=GC����EG=DE+BG����AG��CF����S��FGC=3.6��������ȷ���۵ĸ����ǣ� ��

A��2 B��3 C��4 D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l1��l2 �� ֱ��l3��ֱ��l1��l2���ڵ�C��D����P��ֱ��l3��һ���� 
��1����ͼ1������P���߶�CD���˶�ʱ����PAC����APB����PBD֮�����ʲô������ϵ�����������۲�˵�����ɣ�
��2������P��C��D���������˶�ʱ��P�����C��D���غϣ���ͼ2��ͼ3����������1���еĽ����Ƿ�����������������ֱ��д����PAC����APB����PBD֮���������ϵ������д���ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� ![]() ��m+n+3������ƽ������
��m+n+3������ƽ������ ![]() ��m+2n������������B-A���������ǣ� ��
��m+2n������������B-A���������ǣ� ��
A.1
B.-1
C.0
D.��ȷ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com