
【题目】如图1,AB为⊙O的直径,C为⊙O上一点,D为BC延长线一点,且BC=CD,直线CE与⊙O相切于点C,与AD相交于点E.
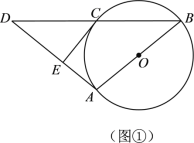
(1)求证:CE⊥AD;
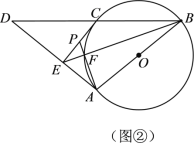
(2)如图2,设BE与⊙O交于点F,AF的延长线与CE交于点P.
①求证:∠PCF=∠CBF;
②若PF=6,tan∠PEF=![]() ,求PC的长.
,求PC的长.
【答案】(1)证明见解析;(2)①证明见解析;②10
【解析】
(1)连结OC,说明OC是△BDA的中位线,利用中位线的性质,得到∠OCE=∠CED=90°,从而求解;
(2)①作直径CG,连结FG,由圆周角定理求得∠G+∠FCG=90°,然后结合(1)求得∠OCE=∠PCF+∠FCG=90°,∠G=∠PCF,然后再结合同弧所对的圆周角相等,从而求解;
②连结AC,利用直径上的圆周角,得到△PEF是直角三角形,利用角相等,可得到△PEF∽△PAE,△PCF∽△PAC,然后根据相似三角形的性质求得![]() ,然后根据三角函数及勾股定理求PC的值.
,然后根据三角函数及勾股定理求PC的值.
解:(1)连结OC.
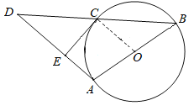
∵直线CE与⊙O相切于点C,
∴OC⊥CE,即∠OCE=90°.
∵OA=OB,BC=CD,
∴C是BD的中点,O是AB的中点,
∴OC是△BDA的中位线,
∴OC∥AD,
∴∠CED=∠OCE=90°,
即CE⊥AD
(2)①作直径CG,连结FG,
∵CG是直径,点F在圆上,
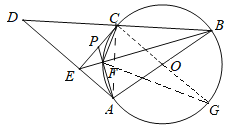
∴∠CFG=90°,
∴∠G+∠FCG=90°.
由(1)可知∠OCE=∠PCF+∠FCG=90°,
∴∠G=∠PCF.
又∵∠G=∠CBF,
∴∠PCF=∠CBF
②连结AC.
∵AB是直径,点F在圆上,
∴∠AFB=∠PFE=90°=∠CEA.
又∵∠EPF=∠APE,
∴△PEF∽△PAE,
∴![]() ,即PE2=PF×PA.
,即PE2=PF×PA.
在直角△PEF中,tan∠PEF=![]() ,
,
又∵PF=6,
∴EF=8,
由勾股定理,可求得PE=10.
∵∠FBC=∠PCF=∠CAF,∠CPF=∠APC
∴△PCF∽△PAC,
∴![]() ,即PC2=PF×PA,
,即PC2=PF×PA,
∴PC2=PE2,
则PC=PE=10


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
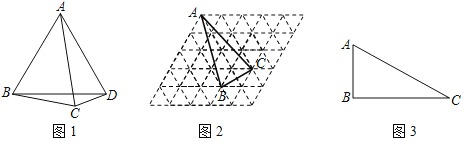
【题目】定义:有一组邻边均和一条对角线相等的四边形叫做邻和四边形.
(1)如图1,四边形ABCD中,∠ABC=70°,∠BAC=40°,∠ACD=∠ADC=80°,求证:四边形ABCD是邻和四边形.
(2)如图2,是由50个小正三角形组成的网格,每个小正三角形的顶点称为格点,已知A,B,C三点的位置如图,请在网格图中标出所有的格点D,使得以A,B,C,D为顶点的四边形为邻和四边形.
(3)如图3,△ABC中,∠ABC=90°,AB=4,BC=4![]() ,若存在一点D,使四边形ABCD是邻和四边形,求邻和四边形ABCD的面积.
,若存在一点D,使四边形ABCD是邻和四边形,求邻和四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
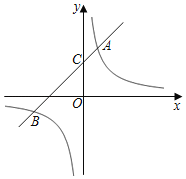
【题目】如图,在平面直角坐标系内xOy中,某一次函数的图象与反比例函数的y=![]() 的图象交于A(1,m)、B(n,﹣1)两点,与y轴交于C点.
的图象交于A(1,m)、B(n,﹣1)两点,与y轴交于C点.
(1)求该一次函数的解析式;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
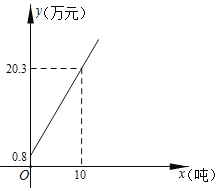
A公司方案:无纺布的价格y(万元)与其重量x(吨)是如图所示的函数关系;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
(1)求如图所示的y与x的函数解析式;(不要求写出定义域)
(2)如果甲厂所需购买的无纺布是40吨,试通过计算说明选择哪家公司费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学进校时需要从学校大门A、B、C三个入口处中的任意一处测量体温,体温正常方可进校.
(1)甲同学在A入口处测量体温的概率是 ;
(2)求甲、乙两位同学在同一入口处测量体温的概率.(用“画树状图”或“列表”的方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实践小组想利用镜子的反射测量池塘边一棵树的高度AB.测量和计算的部分步骤如下:

①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的距离CD=2米,小明的眼睛E到地面的距离ED=1.5米;
②将镜子从点C沿BC的延长线向后移动10米到点F处,小明向后移动到点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH=3米;
③计算树的高度AB;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com