
分析 (1)设乙型清雪车每天各清理路段x千米,根据甲型清雪车清理90千米与乙型清雪车清理60千米路段所用的时间相同,列方程求解;
(2)设购买甲型清雪车a台,则购买乙种型号清雪车(20-a)台,根据购款不超过360万元,列不等式求解.
解答 解:(1)设乙型清雪车每天各清理路段x千米,
根据题意得,$\frac{90}{x+6}$=$\frac{60}{x}$,
解此方程得:x=12,
经检验:x=12是原方程的解,
∴x+6=18.
答:甲型清雪车每天清理路段18千米,乙型清雪车每天清理路段12千米;
(2)设购买甲型清雪车a台,根据题意得:
30a+15(20-a)≤360,
解得:a≤4.
答:最多可购买甲型清雪车4台.
点评 本题考查了分式方程和一元一次不等式的应用,解答本题的关键是读懂题意,射出未知数,找出合适的等量关系,列方程求解,注意检验.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
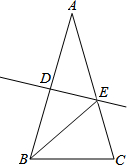 如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )
如图,AB=AC,∠A=40°,AB的垂直平分线DE交AC于点E,垂足为D,则∠EBC的度数是( )| A. | 30° | B. | 40° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=-4 | B. | x=1 | C. | x1=4,x2=1 | D. | x1=-4,x2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
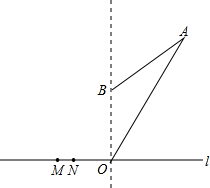 如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)
如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
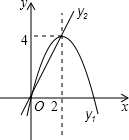 如图,已知抛物线y1=-x2+4x和直线y2=2x,我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.
如图,已知抛物线y1=-x2+4x和直线y2=2x,我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.| A. | ①② | B. | ①②③ | C. | ②③ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com