
����Ŀ������ABC�У�AB=20cm��BC=16cm����DΪ�߶�AB���е㣬����P��2cm/s���ٶȴ�B�����������BC���˶���ͬʱ��Q��a cm/s��a��0��a��2�����ٶȴ�C��������߶�CA���˶������˶�ʱ��Ϊx�룮
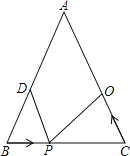
��1����AB=AC��P���߶�BC�ϣ���aΪ��ֵʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�
��2������B=60����������������BDPΪֱ�������Σ�
��3������C=70��������CPQ�Ķ���Ϊ����ʱ����CPQΪ���������Σ�����ֱ��д���𰸣�����д�����̣���
���𰸡���1��![]() cm/s����2����P����2.5���10�����BPDΪֱ�������Σ���3������CPQΪ����������ʱ����CPQ�Ķ���Ϊ35�㣬40�㣬55�㣬70�㣮
cm/s����2����P����2.5���10�����BPDΪֱ�������Σ���3������CPQΪ����������ʱ����CPQ�Ķ���Ϊ35�㣬40�㣬55�㣬70�㣮
��������
�����������1������ȫ��������Ӧ���������̽���֮��Ĺ�ϵ���ٸ���·��=�ٶȡ�ʱ�乫ʽ������õ�P�˶���ʱ�䣬����õ�Q���˶��ٶȣ�
��2��������������ٵ���BPD=90��ʱ������B=60�����õ���BDP=30�������2BP=BD=10�����x=2.5���ڵ���BDP=90��ʱ�����������ε��ڽǺ͵õ���BPD=30�������x=10�����ɵõ���P����2.5���10�����BPDΪֱ�������Σ�
��3���ֵ�P�ڱ�BC�ϻ��P�ڱ�BC���ӳ����ϣ���CPQΪ���������Σ����ݵ��������ε����ʺ������ε��ڽǺͼ��ɵõ����ۣ�
�⣺��1����AB=AC��
���B=��C��
��AB=20cm��D��AB���е㣬
��BD=10cm��
����Q���ٶ����P���ٶȲ�ͬ��
��BP��CQ��
Ҫʹ��BPD����CQPȫ�ȣ�
��BP=CP=8cm CQ=BD=10cm��
��x=![]() �룬
�룬
��a=![]() =
=![]() cm/s��
cm/s��
��2���ٵ���BPD=90��ʱ��
�ߡ�B=60�������BDP=30����
��2BP=BD=10��
��BP=5��
��2x=5��
��x=2.5��
�ڵ���BDP=90��ʱ��
�ߡ�B=60����
���BPD=30����
��BP=2BD=20��
��2x=20��
��x=10��
����P����2.5���10�����BPDΪֱ�������Σ�
��3����P�ڱ�BC�ϣ���CPQΪ���������Σ�
�ٵ�PQ=CQ���ߡ�C=70����
���CPQ=��C=70����
�ڵ�PQ=PC���ߡ�C=70����
���PQC=��C=70����
���CPQ=180����2��70��=40�㣬
�۵�PC=CQ���ߡ�C=70����
���CPQ=��CQP=![]() =55�㣬
=55�㣬
��P�ڱ�BC���ӳ����ϣ���CPQΪ���������Σ�
�ߡ�ACB=70�������ACP=110����
��PC=CQ��
���CPQ=��CQP=![]() =35�㣬
=35�㣬
��������������CPQΪ����������ʱ����CPQ�Ķ���Ϊ35�㣬40�㣬55�㣬70�㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016�㶫ʡ÷���е�1��)���㣨��3��+4�Ľ����( )
A�� ��7 B�� ��1 C�� 1 D�� 7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x2-��m2-4��x+m=0����������Ϊ�෴������m���ڣ�������
A. -2 B. 2 C. ��2 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016����ʡ�����е�11��)����������ʽx2+4x+5���ɣ�x+p��2+q����ʽӦΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����Ŀڴ��з������ɸ�������������������������ɫ֮��û�������κ����������е����Ѿ��������ӿڴ���ȡ��һ����ȡ������ĸ���Ϊ![]() ��
��
��1��ȡ������ĸ����Ƕ��٣�
��2��������еĻ�����12������ô���е������ж��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڽ�����ij�ƶ���˾�ƻ��Ƴ������µļƷѷ�ʽ�����±���ʾ��
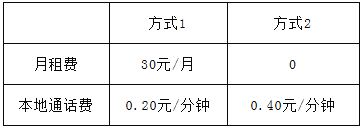
���������������⣺��ͨ��ʱ��Ϊ��������
��1��������ͨ��100���ӣ�����ʽһ�轻�Ѷ���Ԫ������ʽ���轻�Ѷ���Ԫ��
��2������ij�±���ͨ������ͨ���ʱ��ʱ�������ּƷѷ�ʽ���շ�һ���ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=kx-6��������y=ax2+bx+c�ཻ��A��B���㣬�ҵ�
A��1��-4��Ϊ�����ߵĶ��㣬��B��x������ֱ��AB��y���ڵ�D,�����߽�y���ڵ�C��
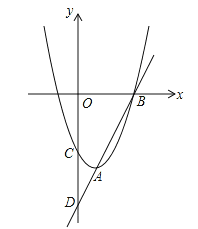
��1����ֱ��AB�Ľ���ʽ��
��2���������ߵĽ���ʽ��
��3����y�����Ƿ���ڵ�Q��ʹ��ABQΪֱ�������Σ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�����Ʒ�ڼס��������̵����ۣ�����ÿ��477Ԫ������۳��ۣ����Ż����ҵ���ÿ��530Ԫ��������IJ�����Ʒ��������3�ˣ������ֿɴ���۳�����������IJ�����Ʒ����Ϊx�ˣ�����x��3��
��1���ֱ��г����ס����̵깺����ֲ�����Ʒ����������ú�x�Ĵ���ʽ��ʾ����
��2�����Ҫ��һ������10�˵Ĵ��в�����Ʒ�����ĸ��̵깺���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com